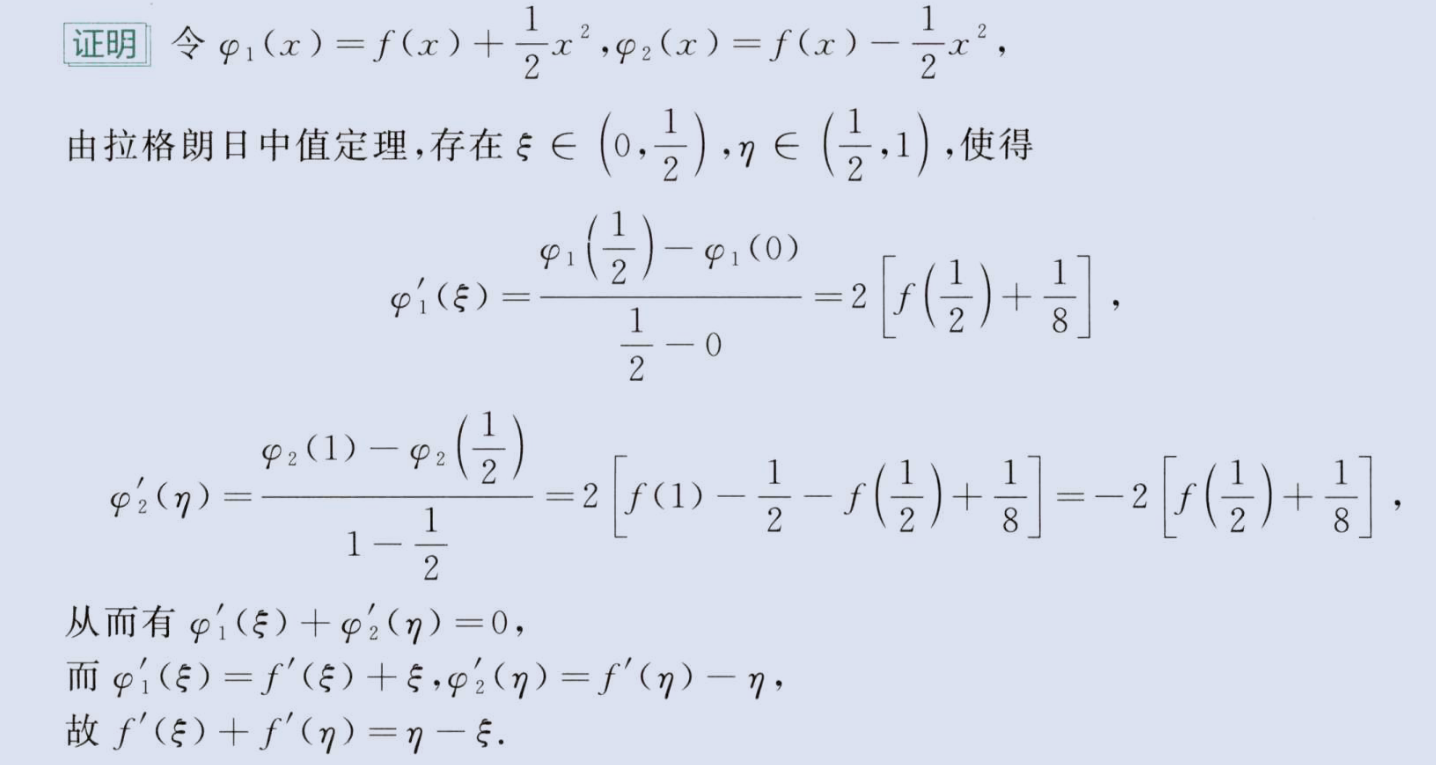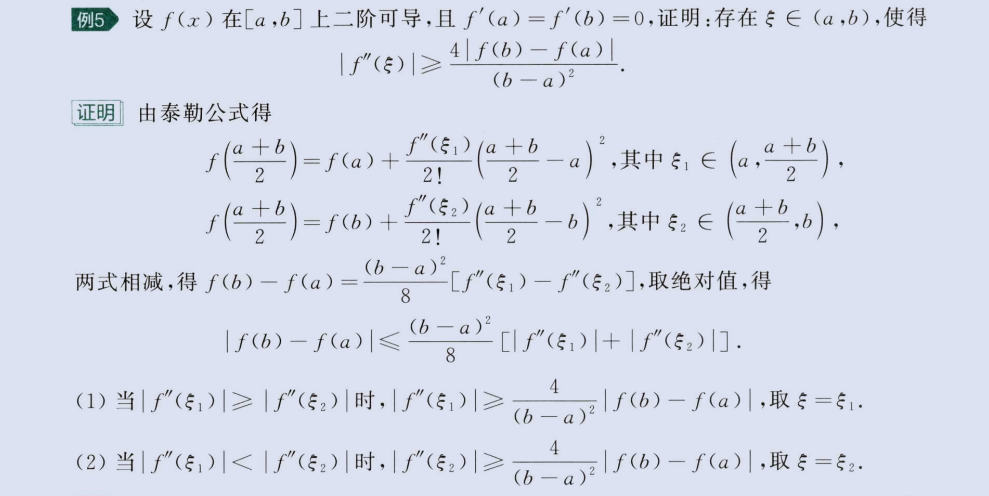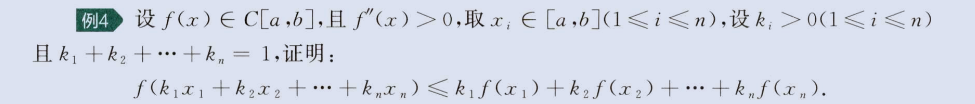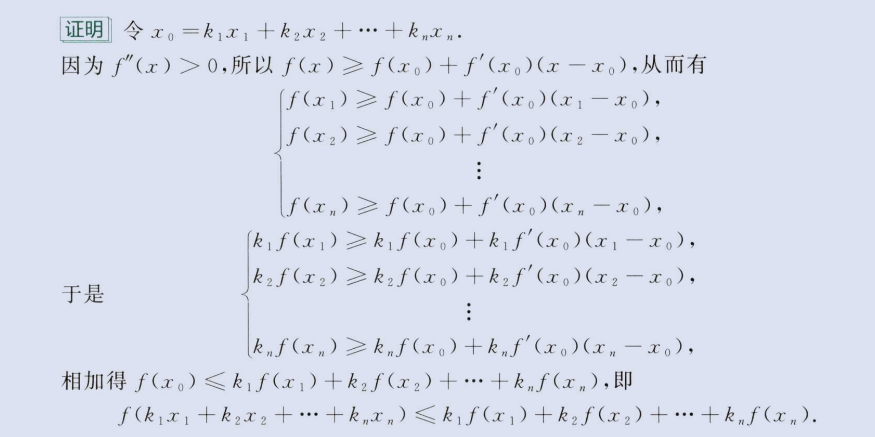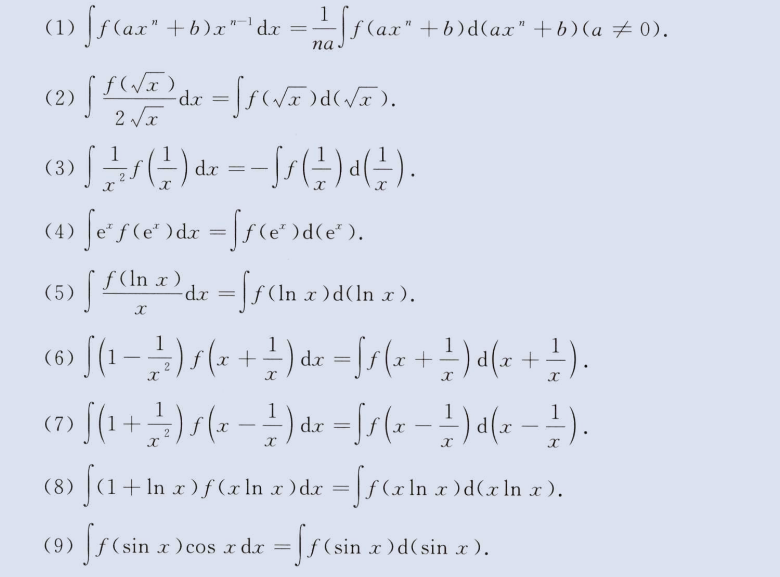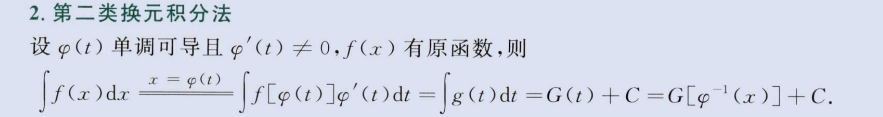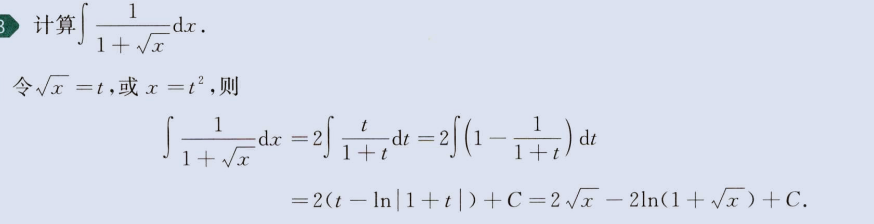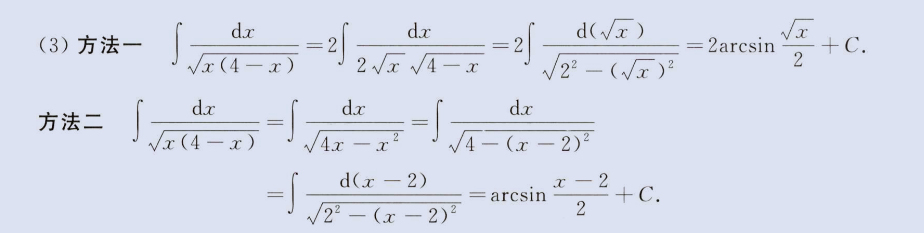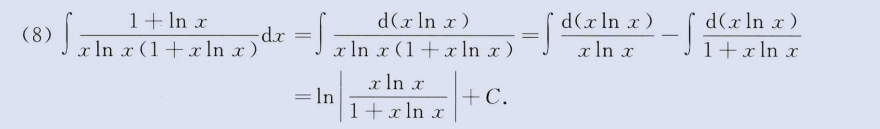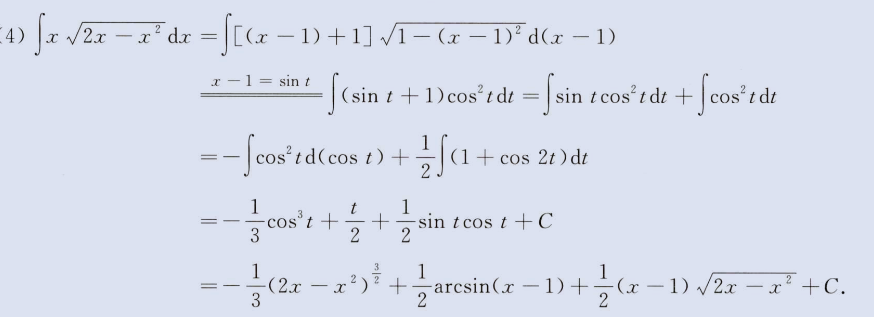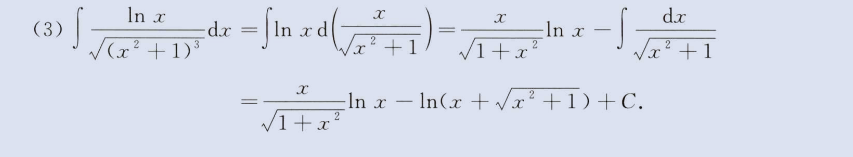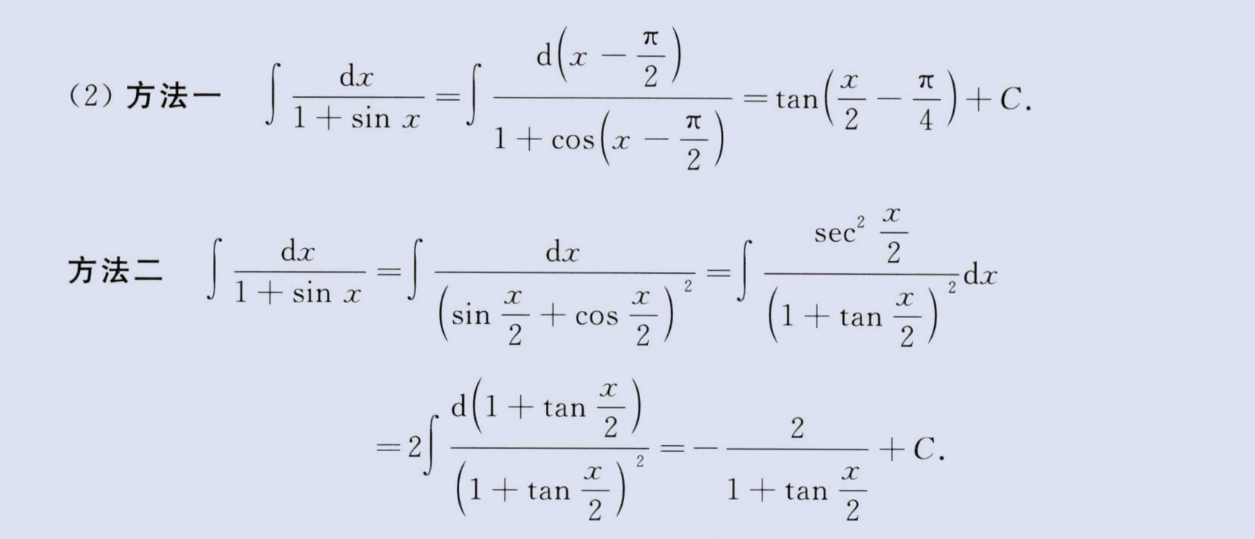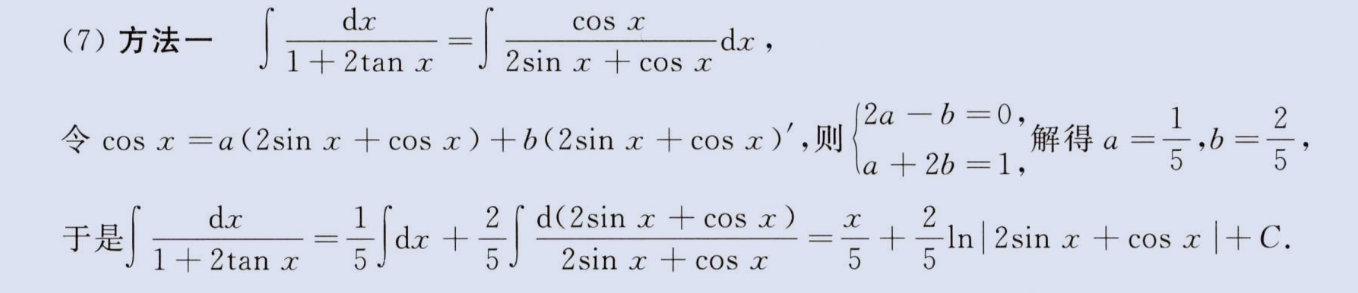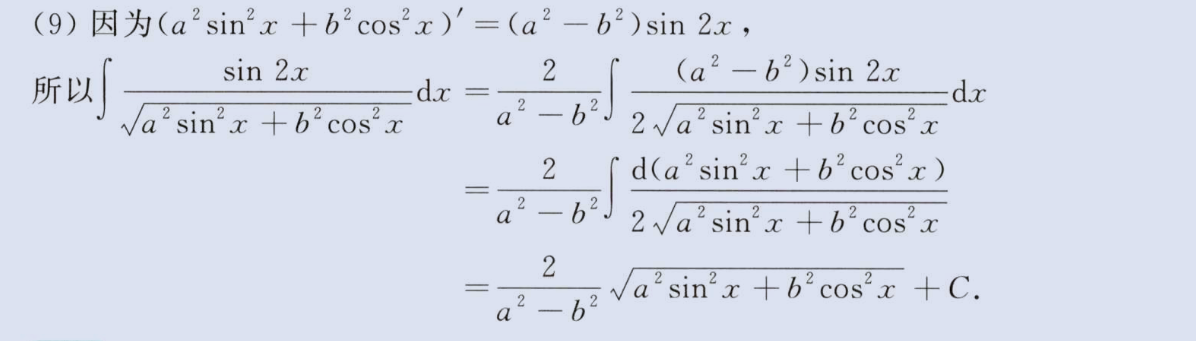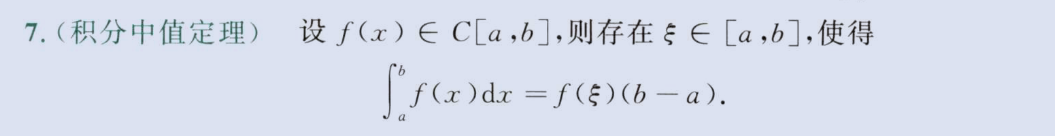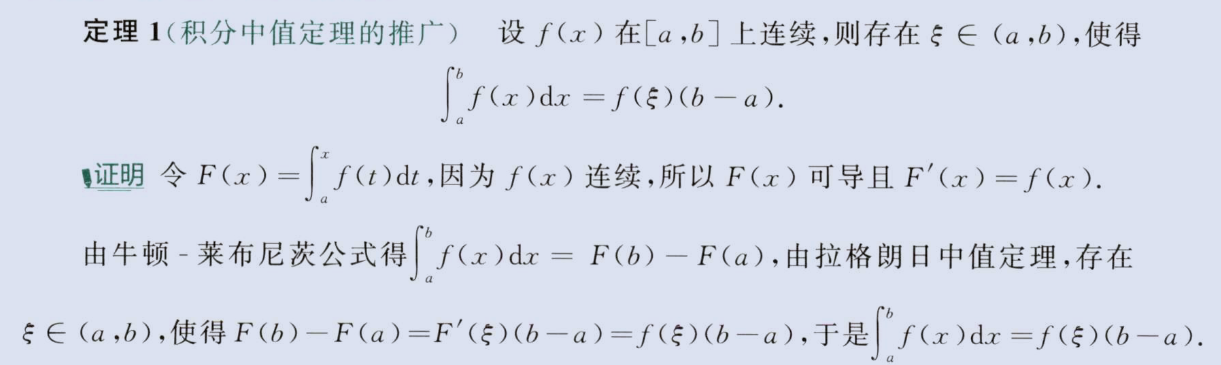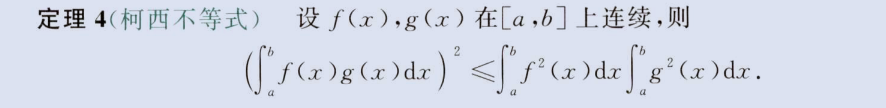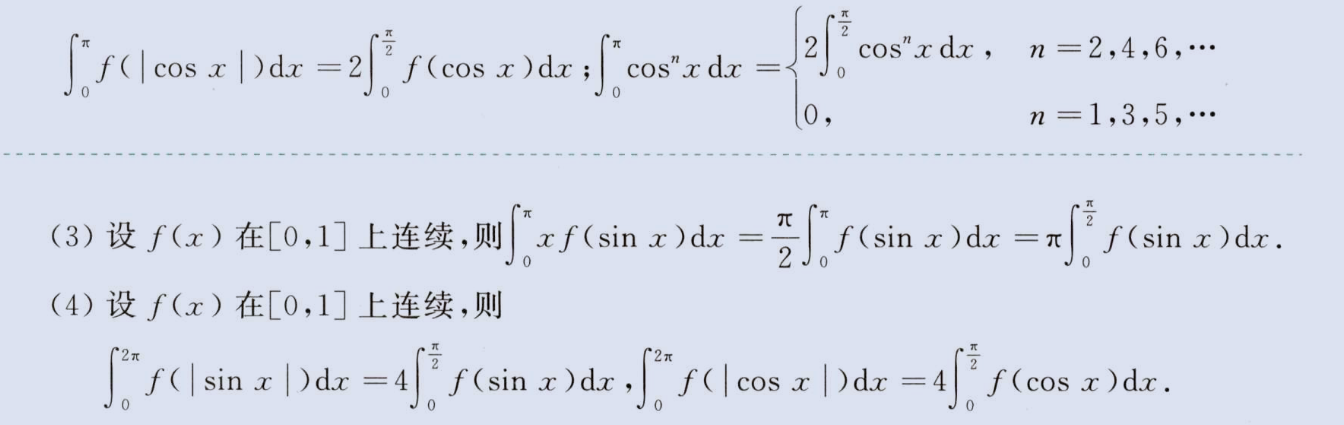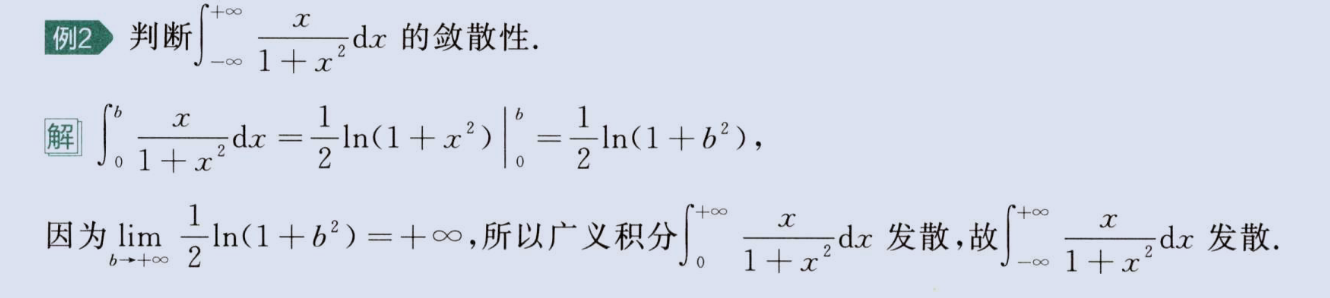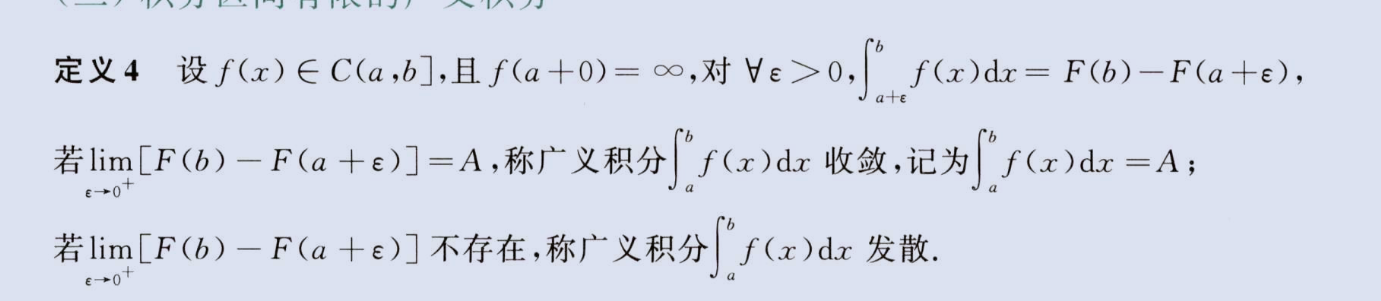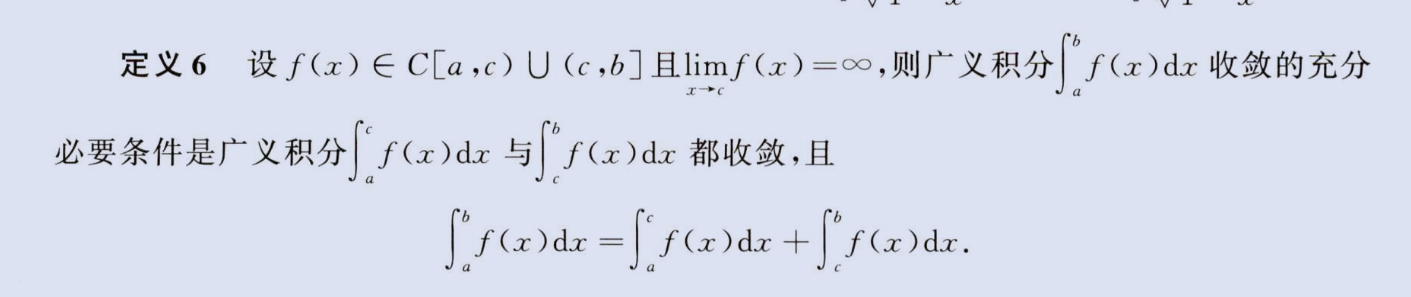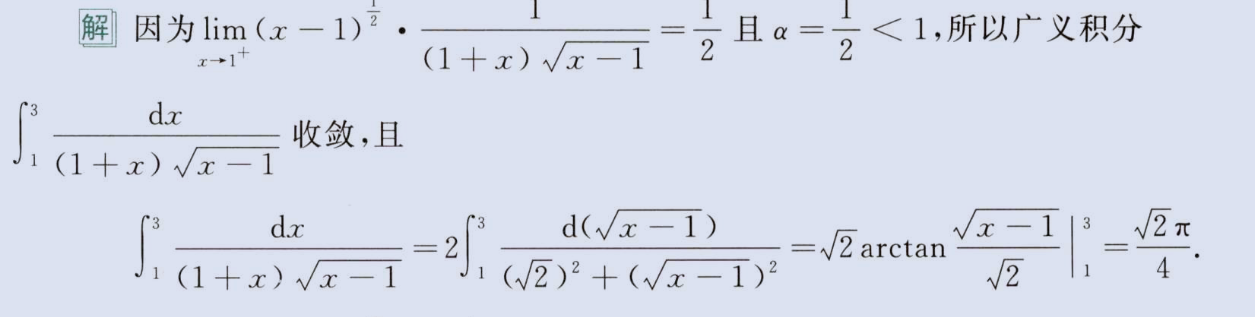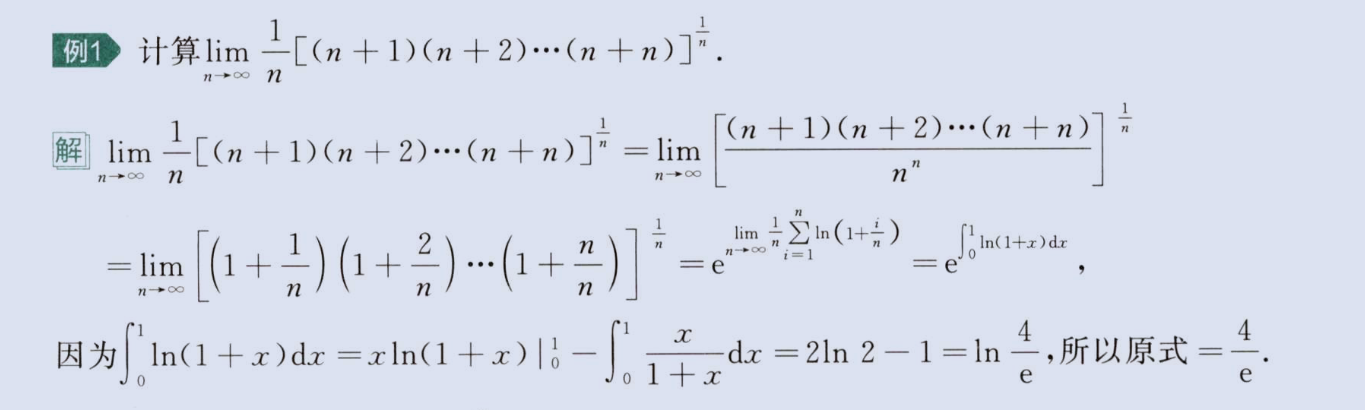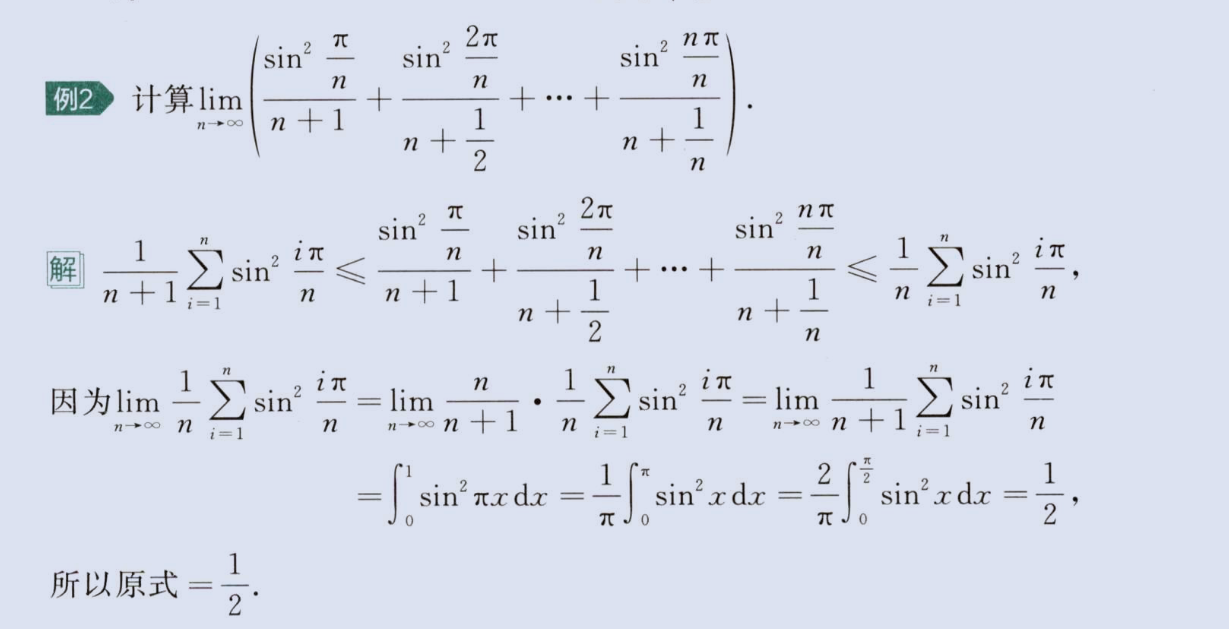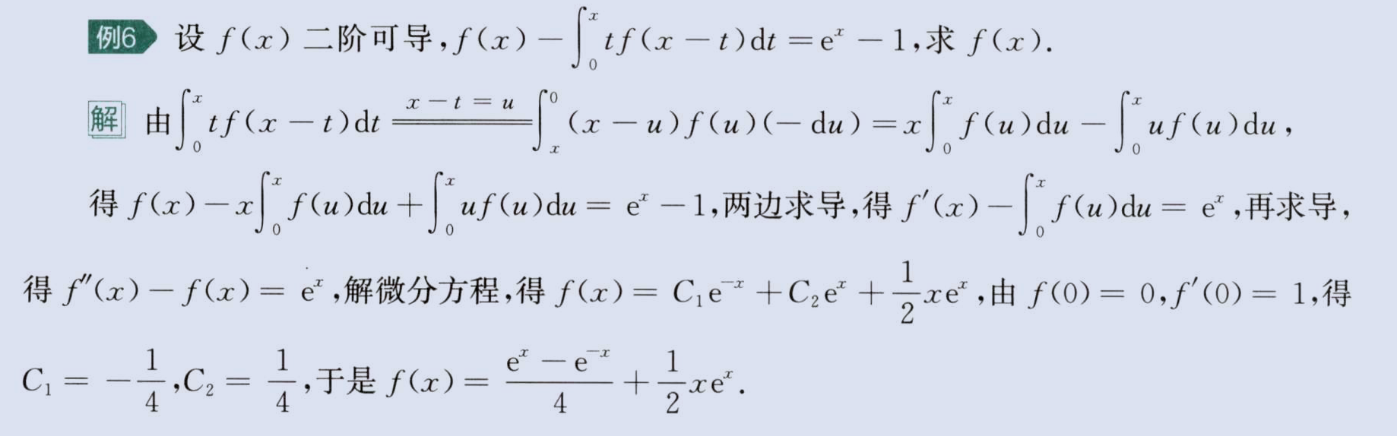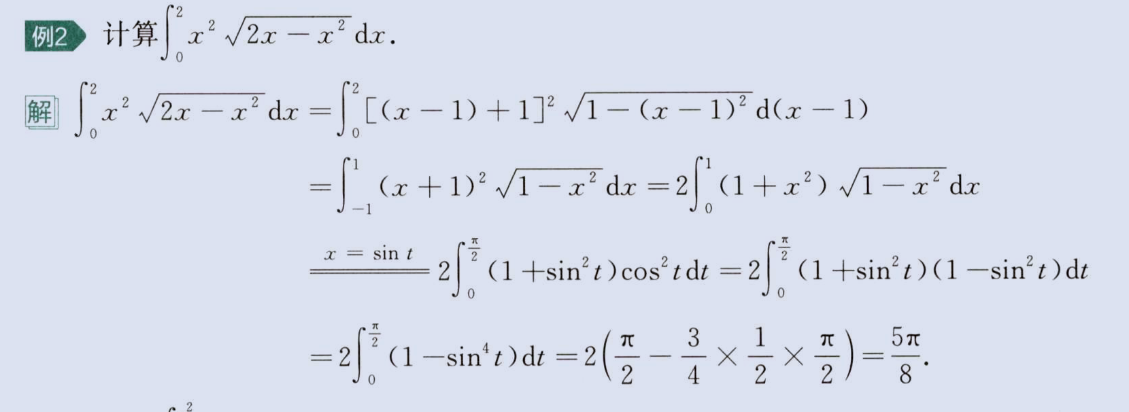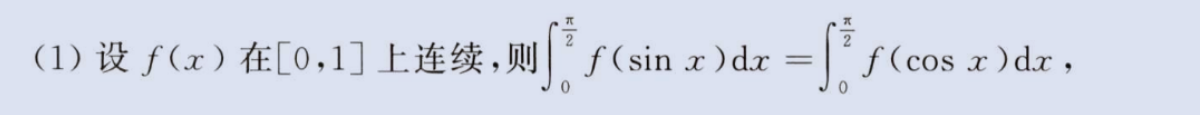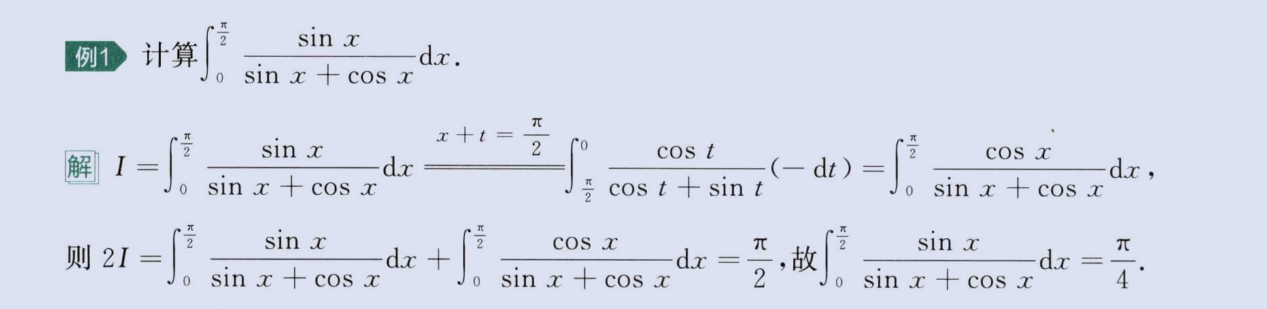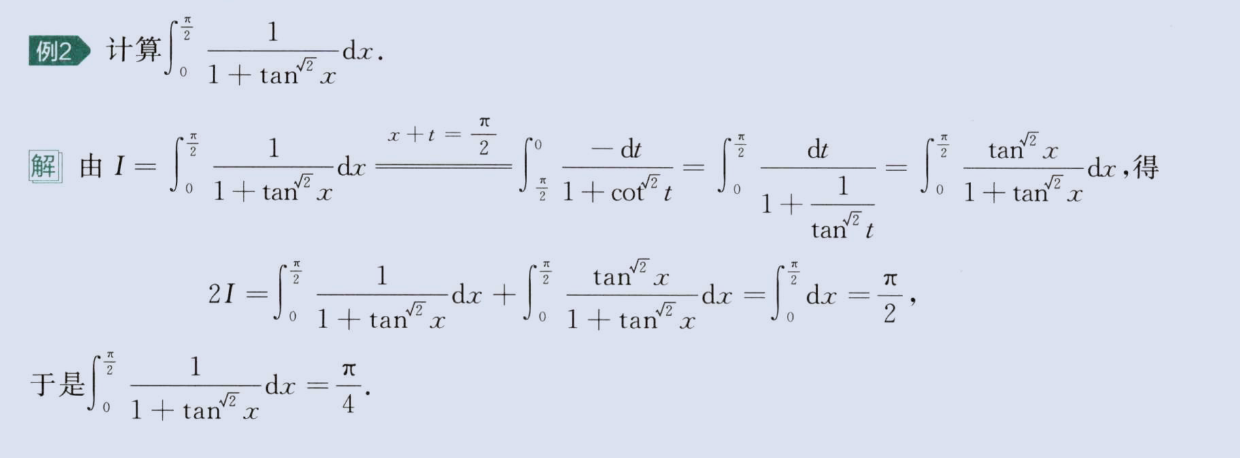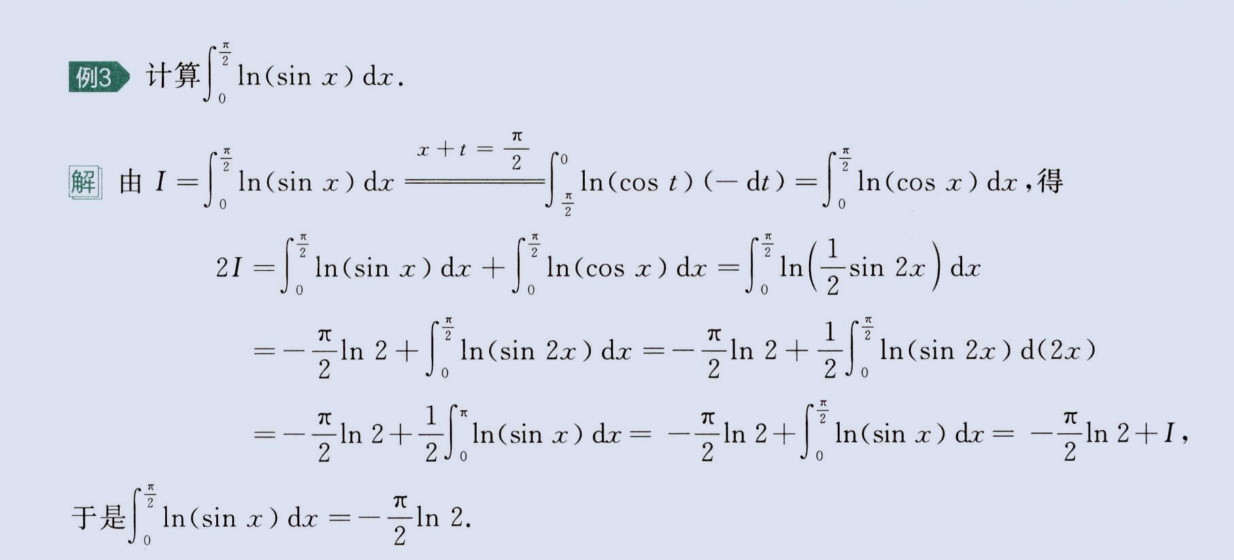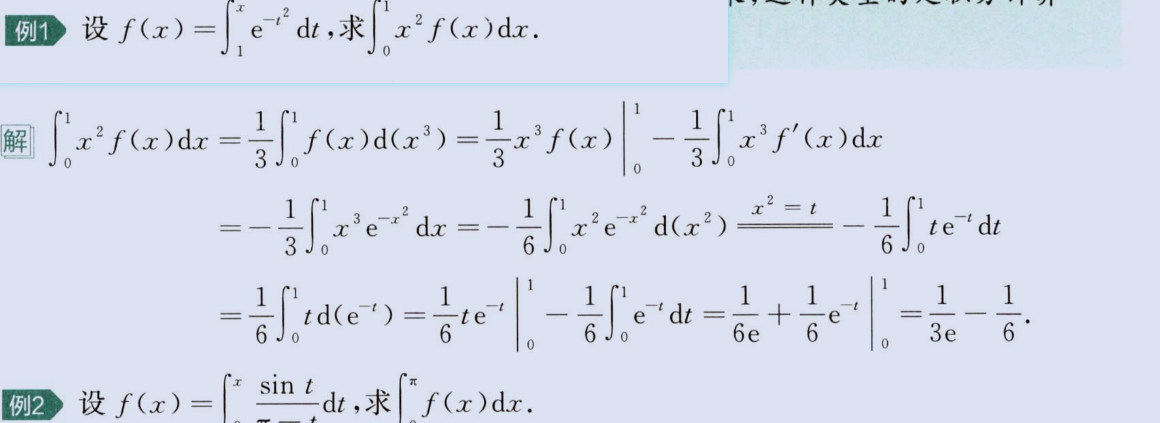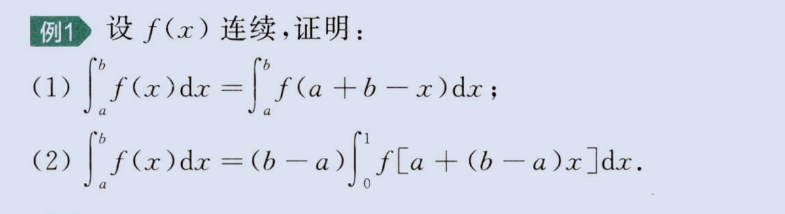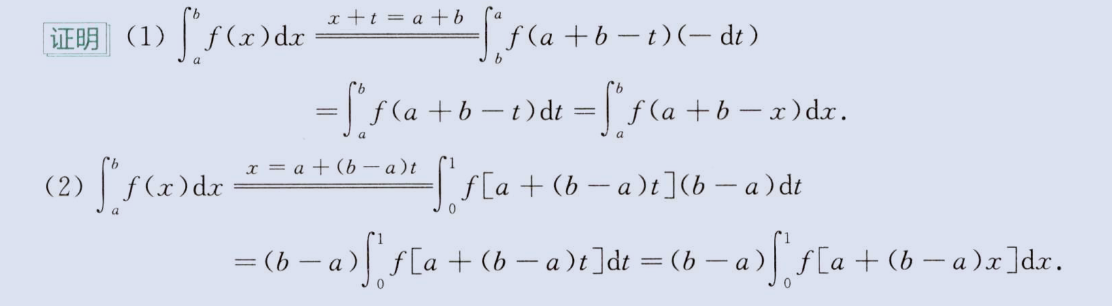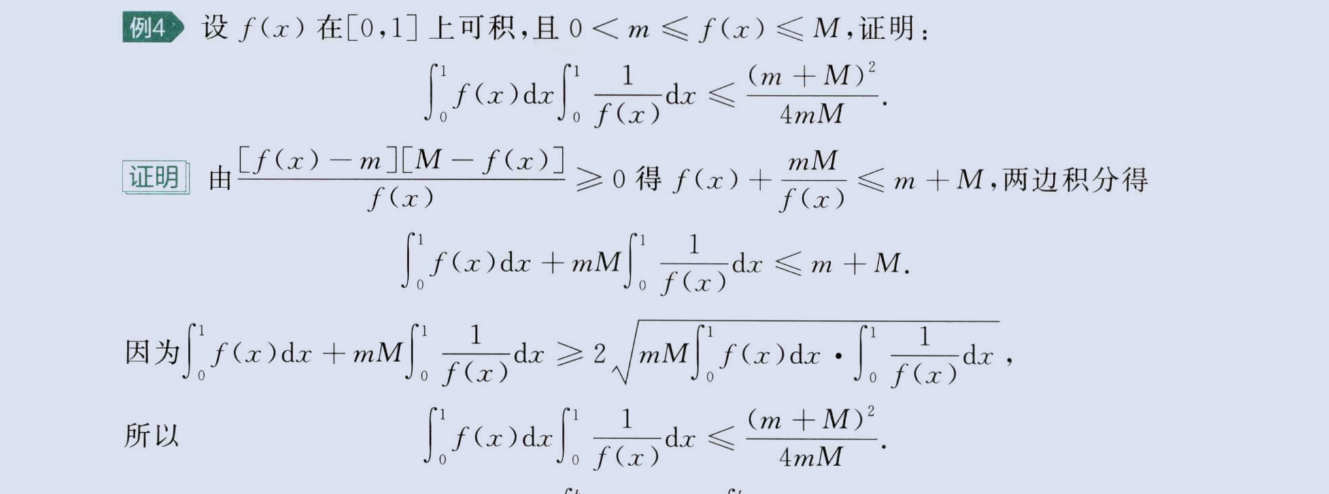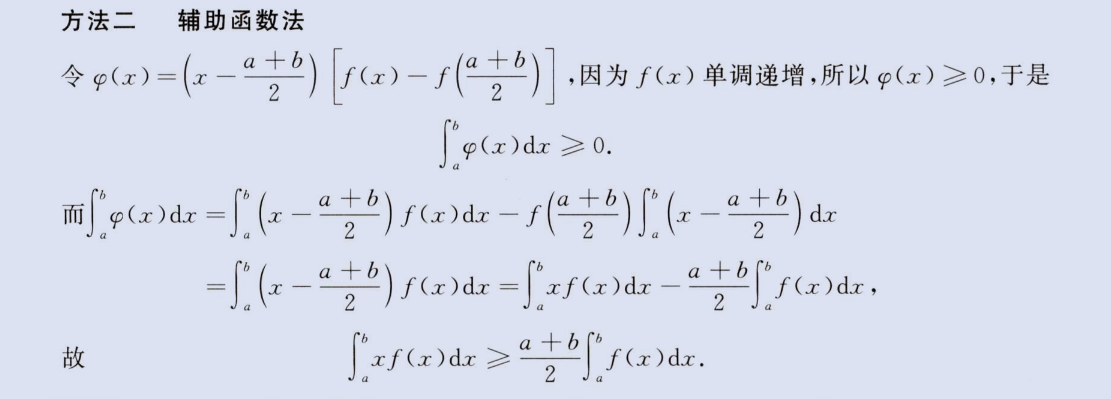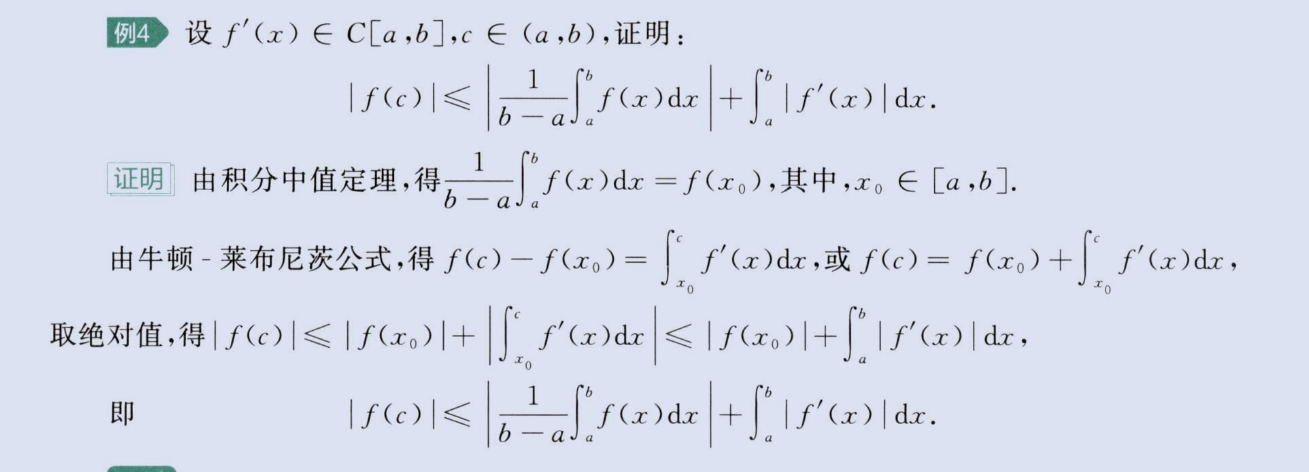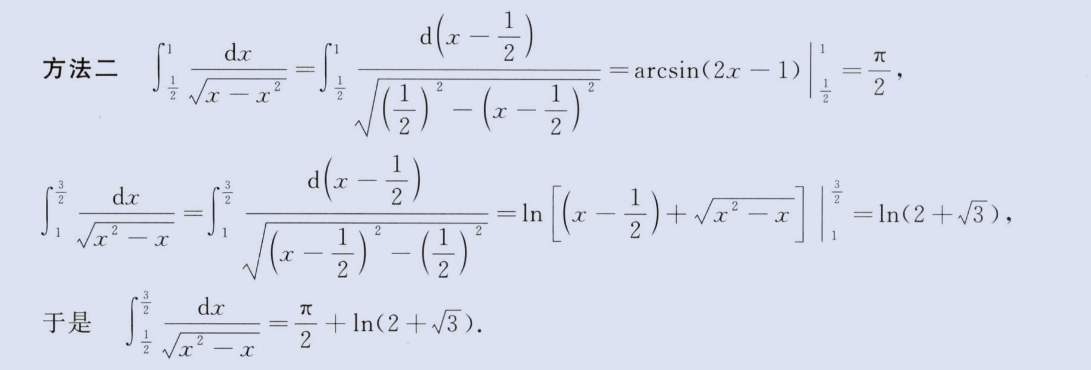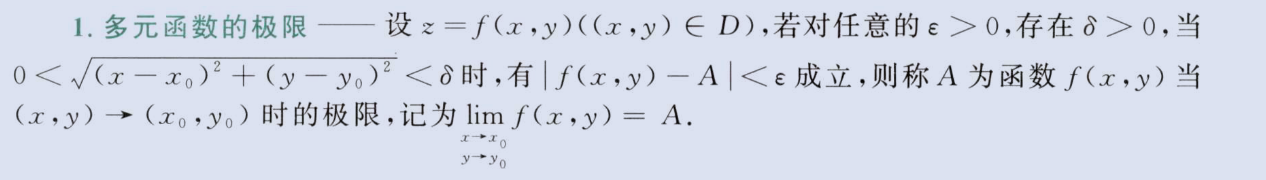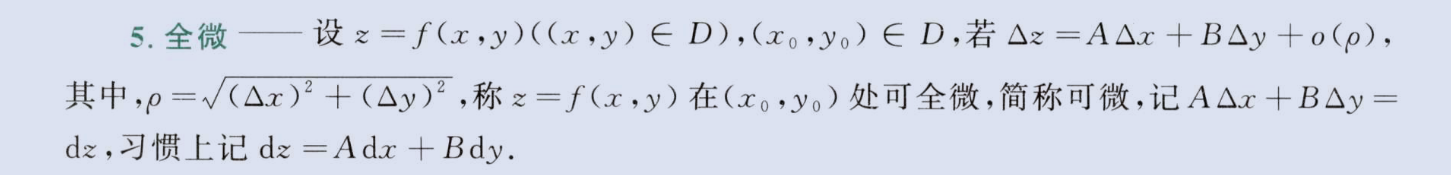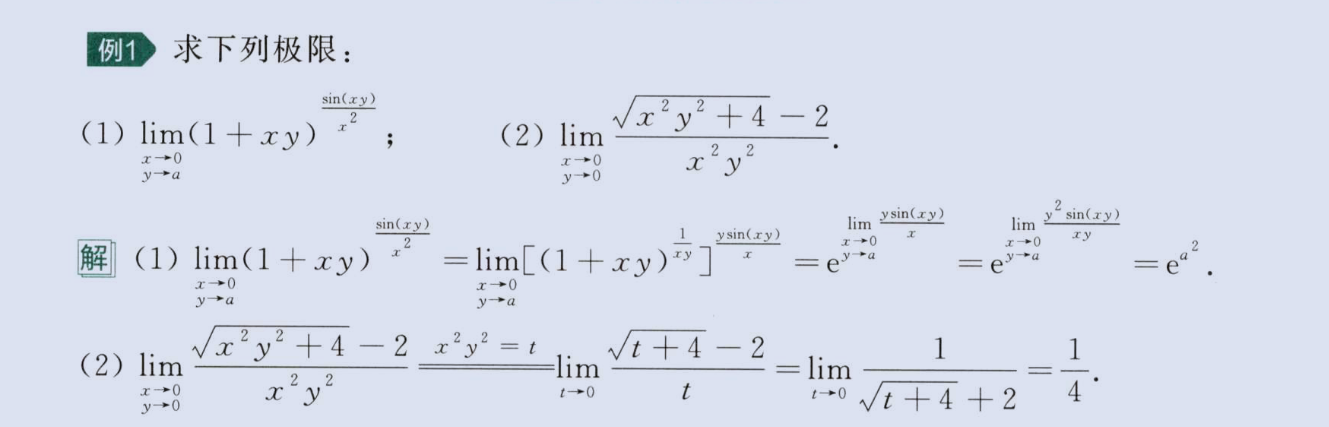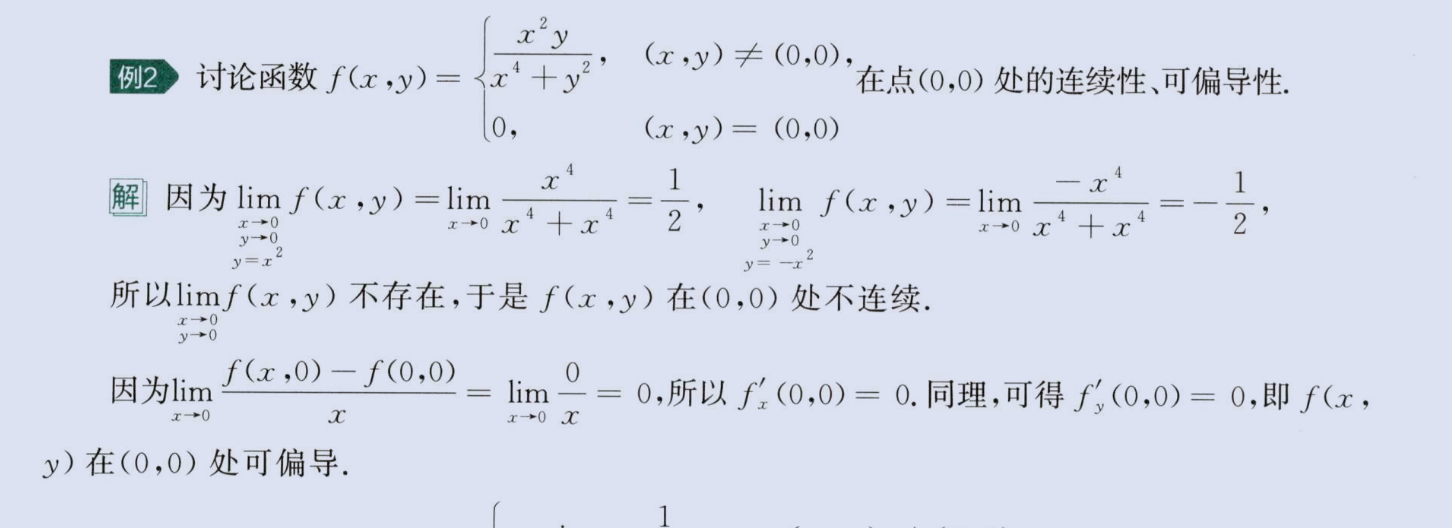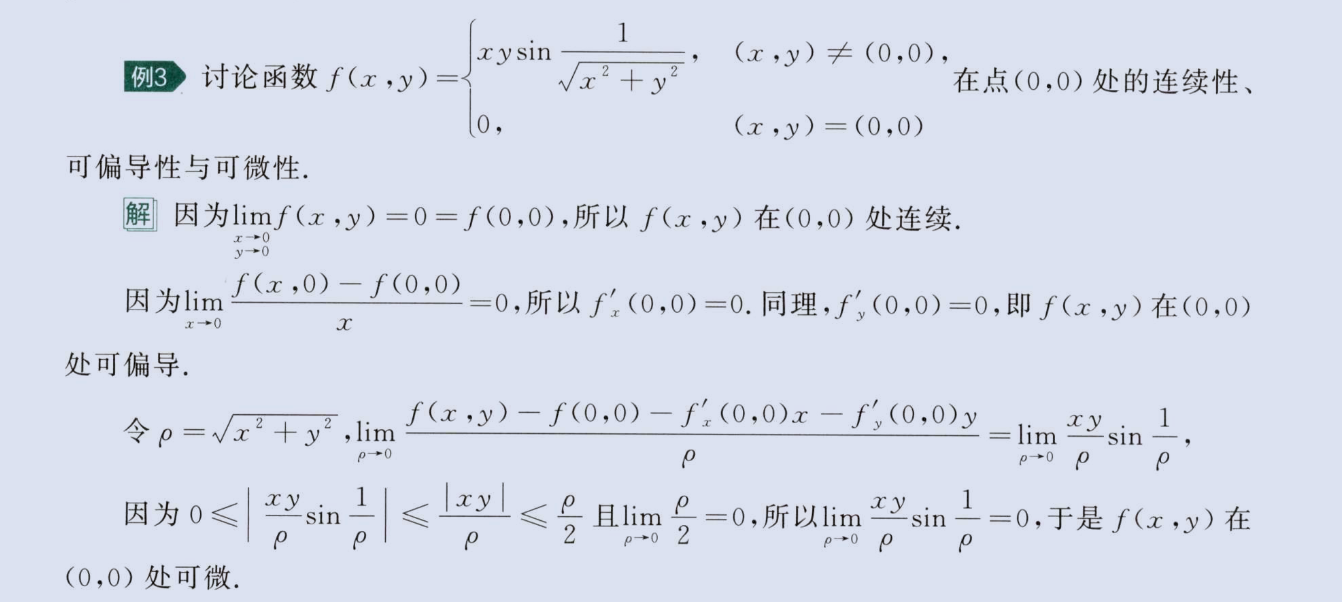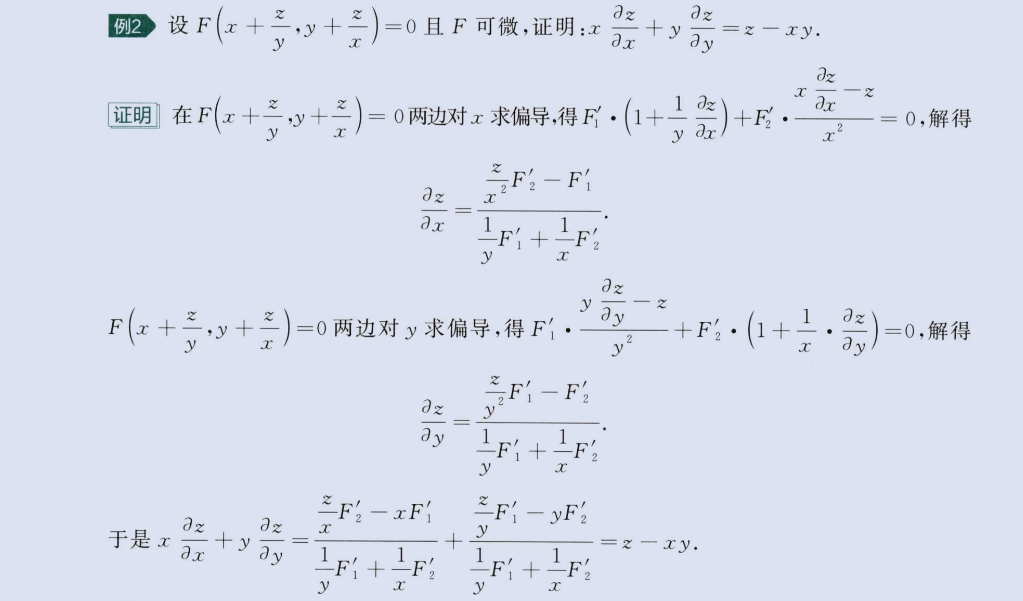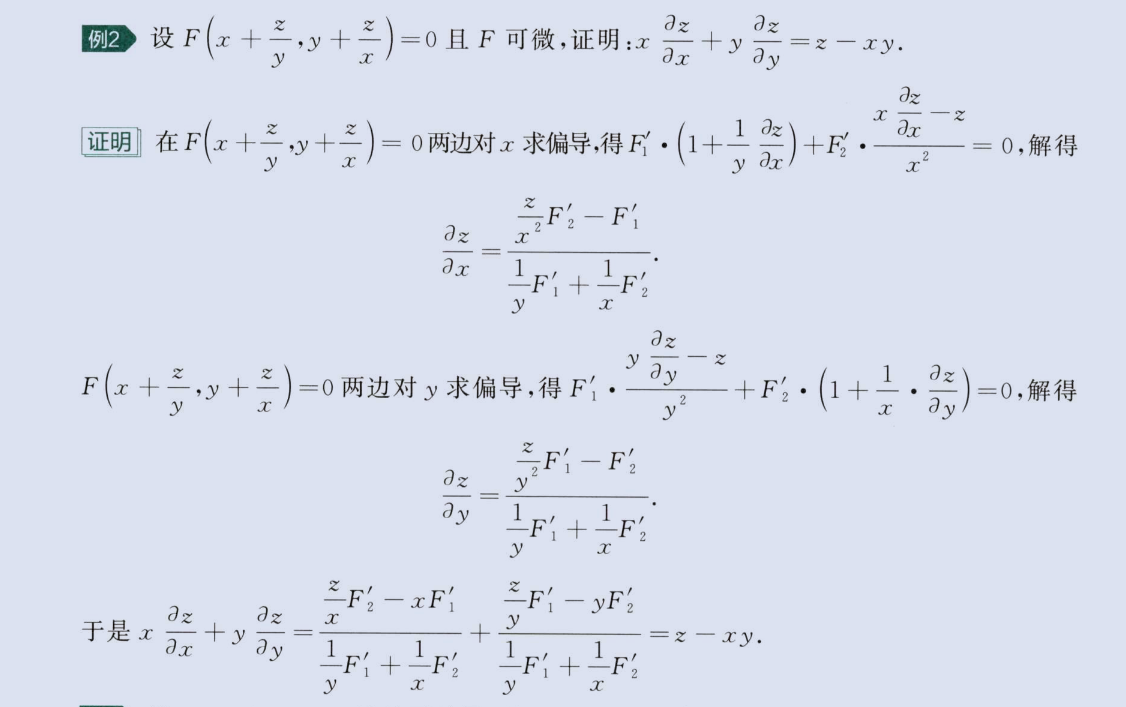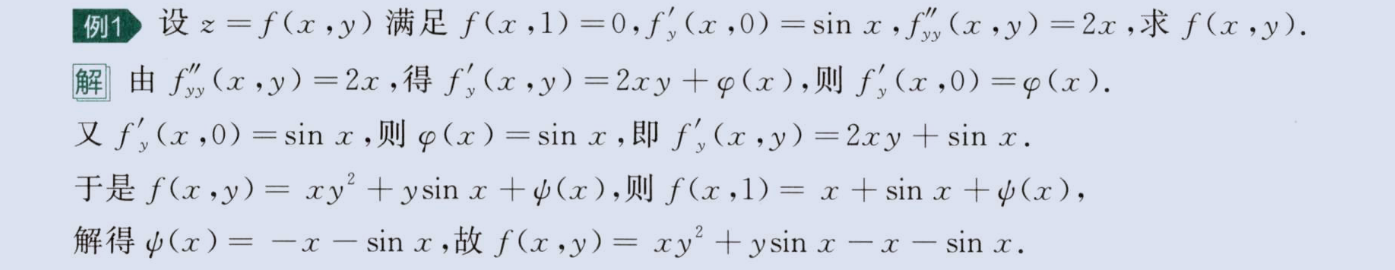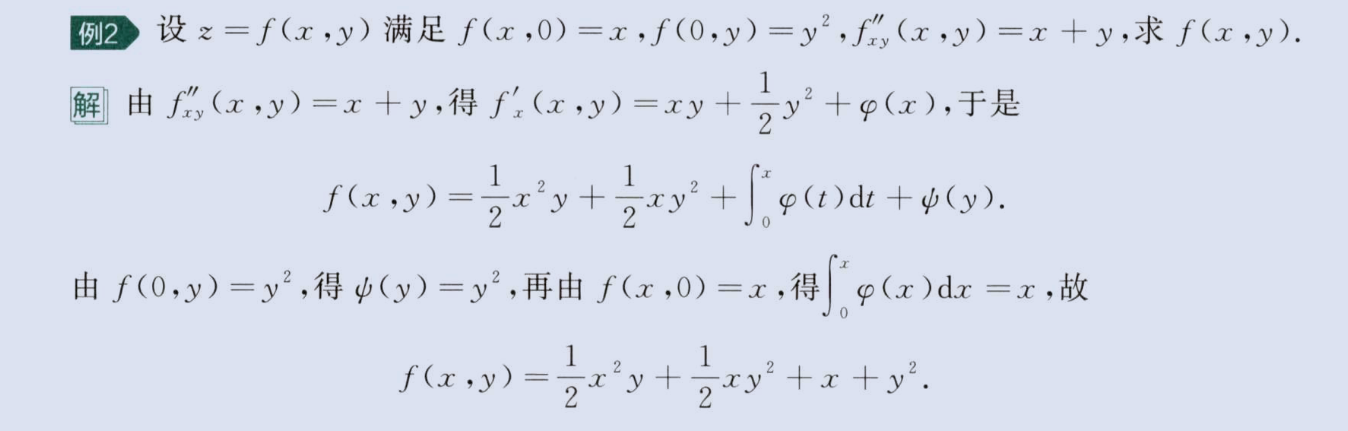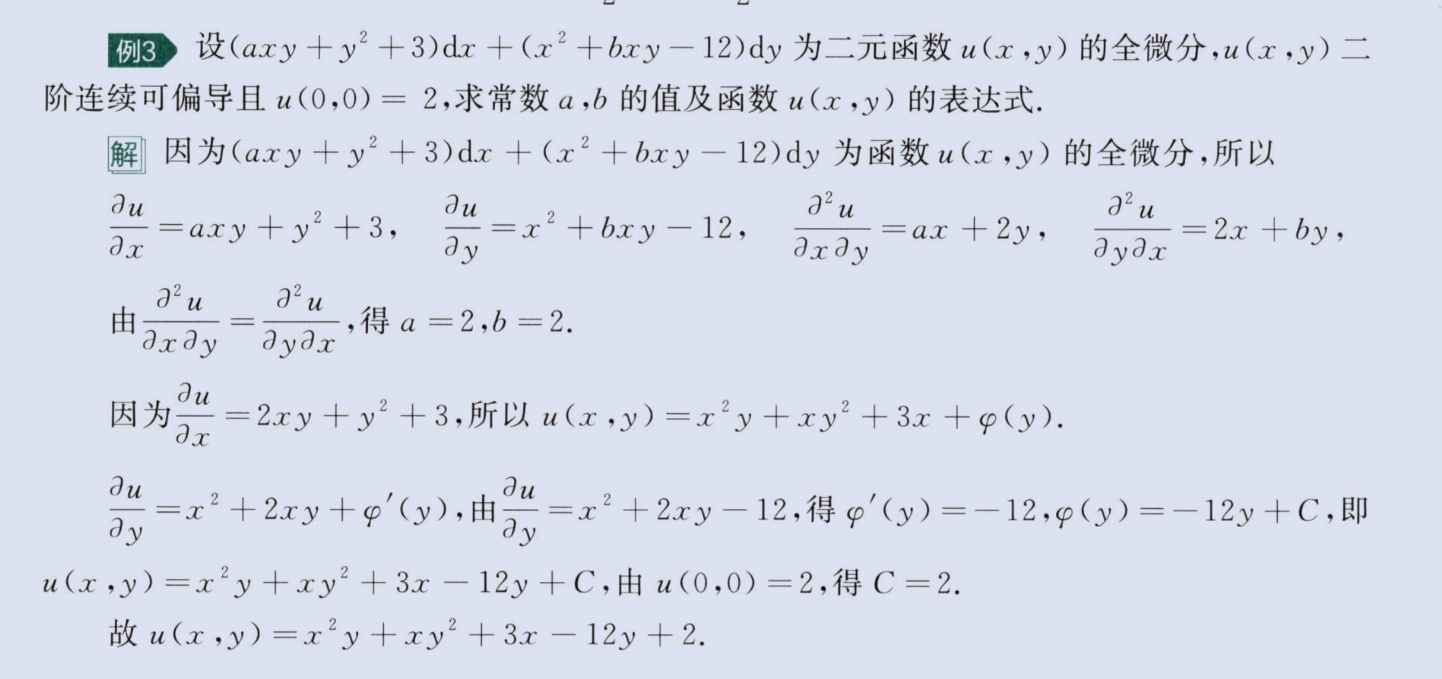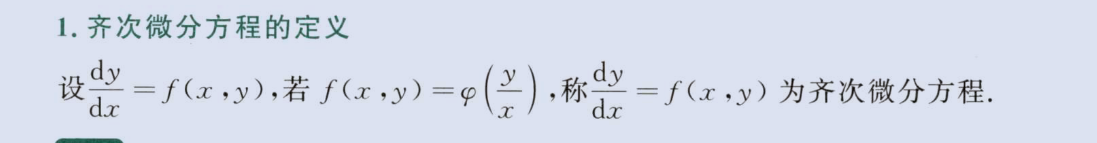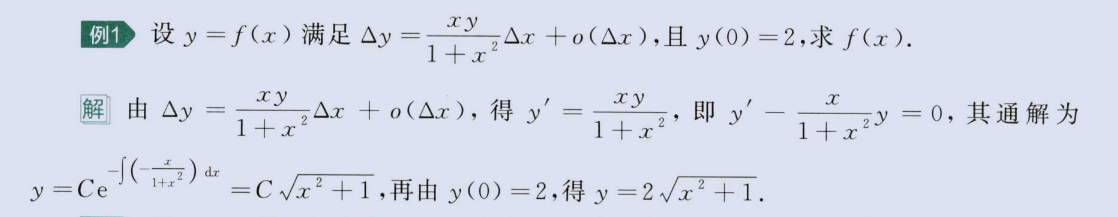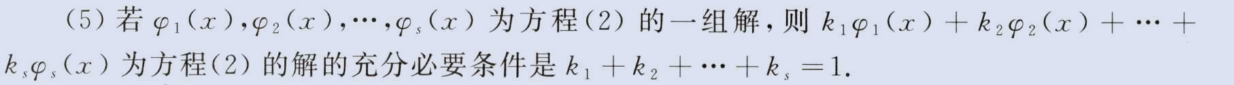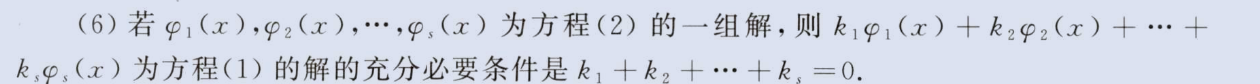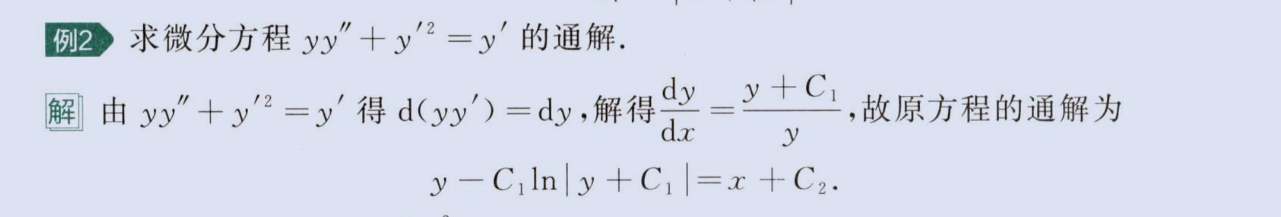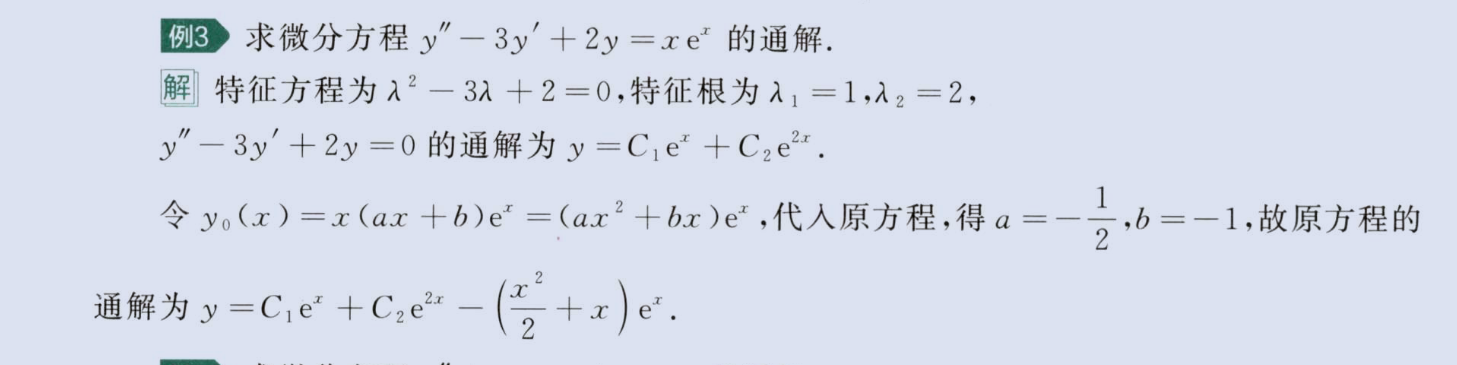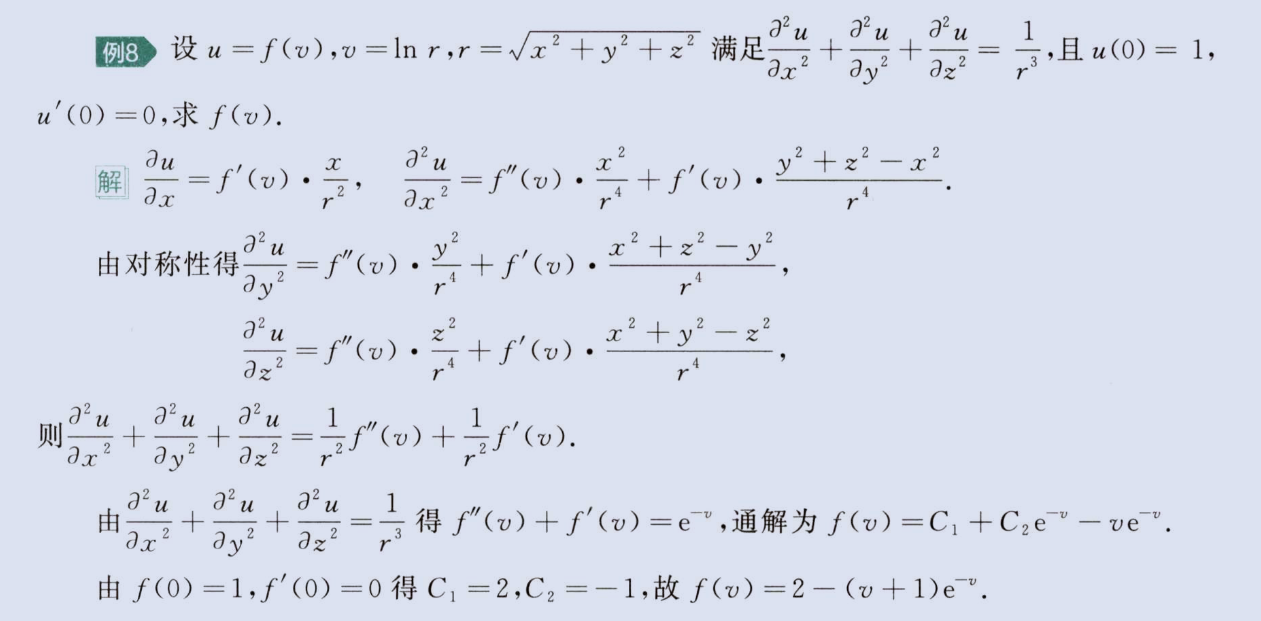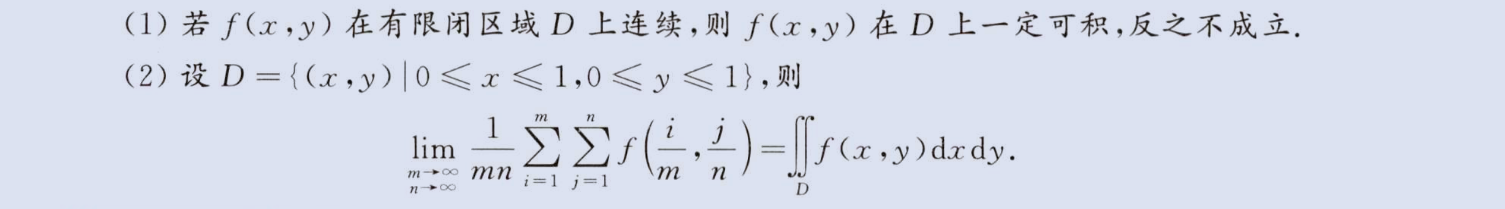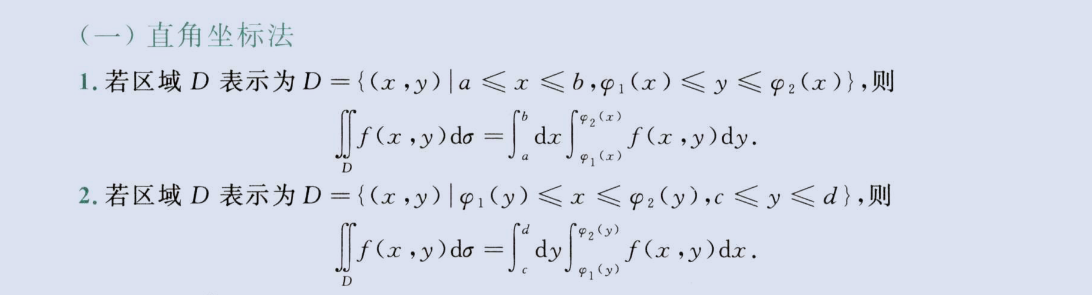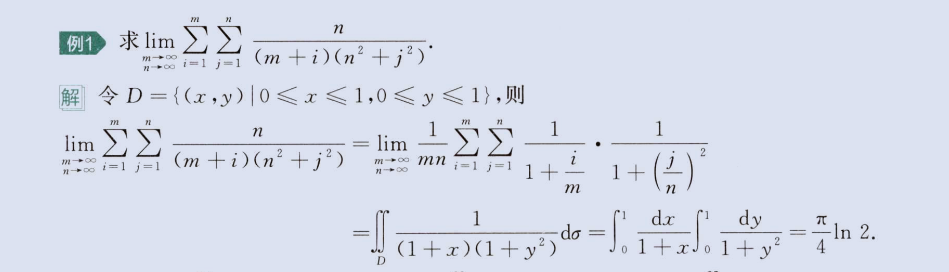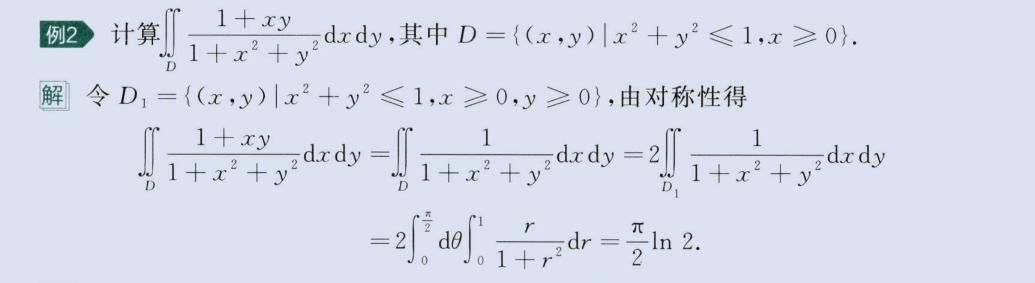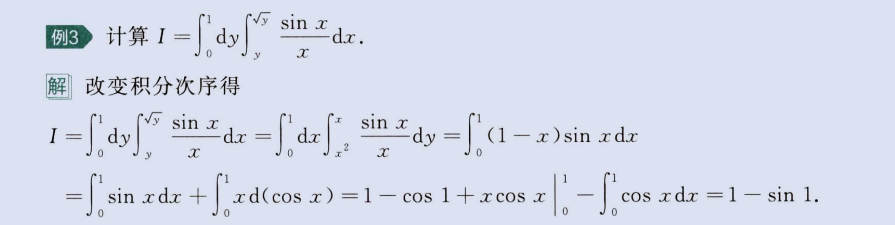网络卡顿请打开备用网址
(flowus.cn)高数 总览
高数
第一章 极限与连续 (flowus.cn)
高数
第二章 导数与微分 (flowus.cn)
高数
第三章 一元函数微分学的应用 (flowus.cn)
高数
第四章 不定积分 (flowus.cn)
高数
第五章 定积分 (flowus.cn)
高数
第六章 多元函数微分学 (flowus.cn)
高数
第七章 微分方程 (flowus.cn)
高数
第八章 重积分 (flowus.cn)
错题笔记
(flowus.cn)
第一章-极限与连续
高数
第一章 极限与连续 (flowus.cn)
知识点
极限
1、定义
 image-20230803163253910
image-20230803163253910
2、性质
 image-20230803163507189
image-20230803163507189
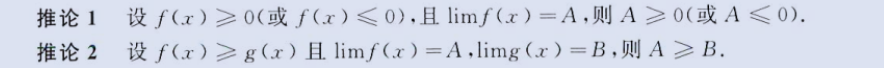 image-20230803163557768
image-20230803163557768
 image-20230803163825302
image-20230803163825302
 image-20230803163919486
image-20230803163919486
 image-20230803163945427
image-20230803163945427
3、常用极限
 image-20230803164241072
image-20230803164241072
无穷小
1、定义
 image-20230803163357862
image-20230803163357862
2、常用无穷小
 image-20230803164119951
image-20230803164119951
x-ln(1+x) ~ x^2/2
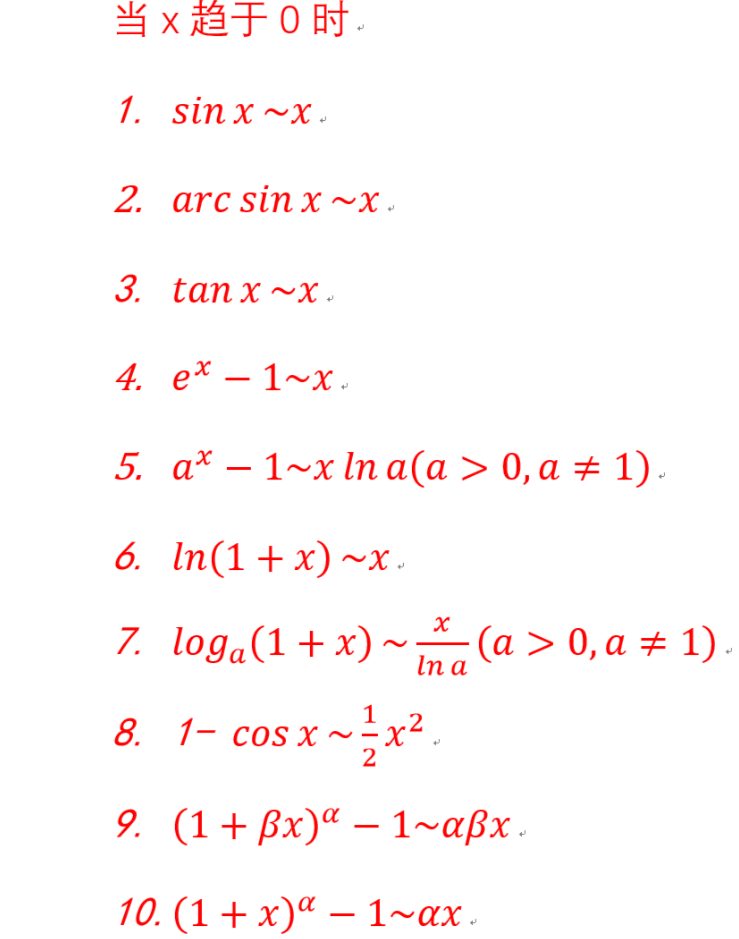 image-20230803185050652
image-20230803185050652
连续
 image-20230803164326504
image-20230803164326504
间断
 image-20230803164425601
image-20230803164425601
 image-20230803164410913
image-20230803164410913
题型
极限是否存在
1、左右极限
 image-20230803162155807
image-20230803162155807
2、单调有界(数学归纳法)
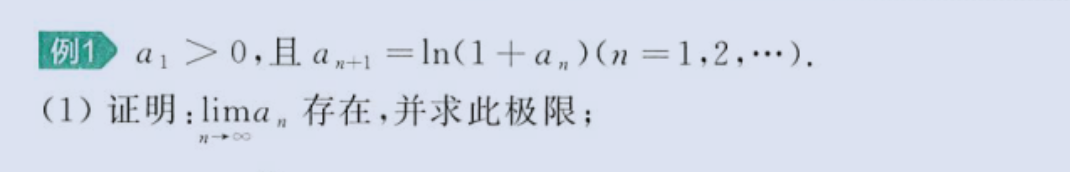 image-20230803181437761
image-20230803181437761
 image-20230803181452663
image-20230803181452663
不定型极限
 image-20230803164620582
image-20230803164620582
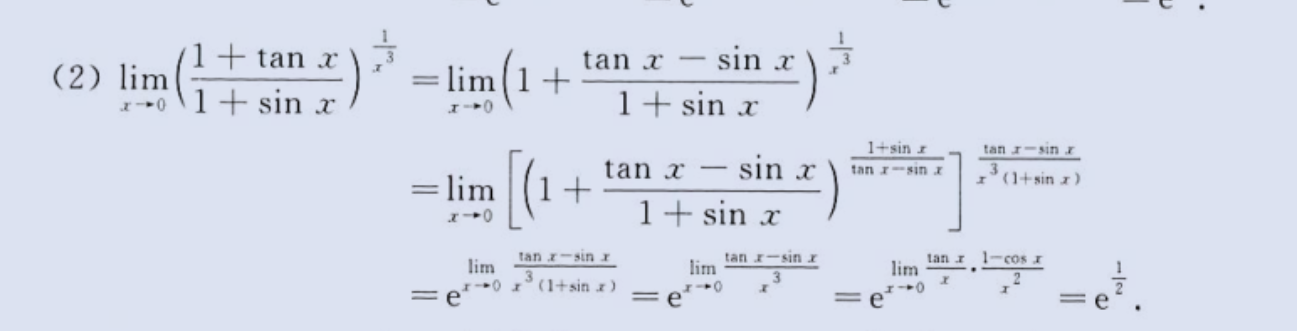 image-20230803181339123
image-20230803181339123
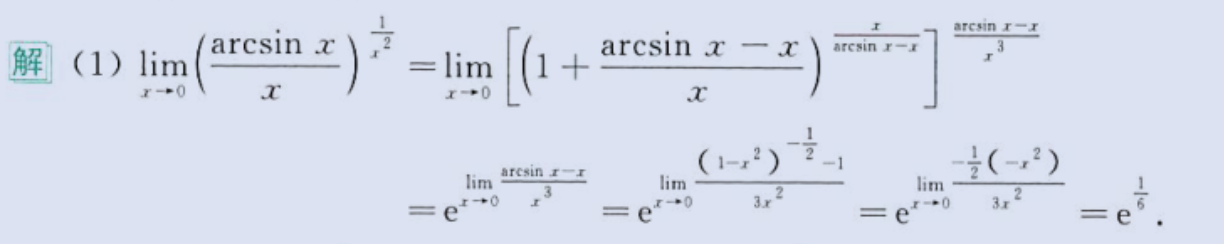 image-20230803181047573
image-20230803181047573
n 项 和、积的极限
 image-20230803164819474
image-20230803164819474
添项合并求极限
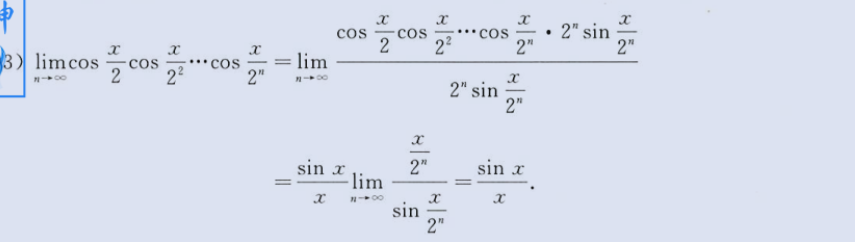 image-20230803165028219
image-20230803165028219
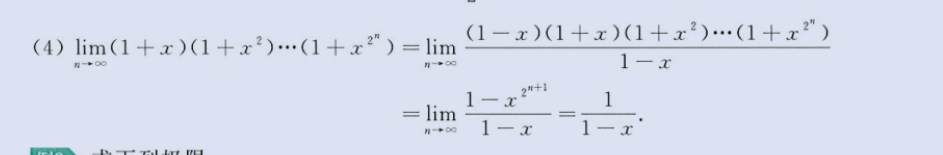 image-20230803165109178
image-20230803165109178
夹逼定理(放缩)求极限
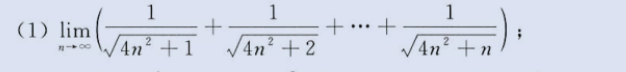 image-20230803165327815
image-20230803165327815
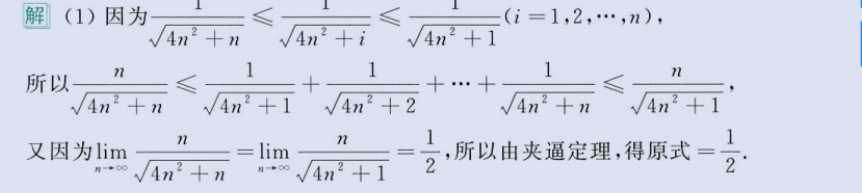 image-20230803165234759
image-20230803165234759
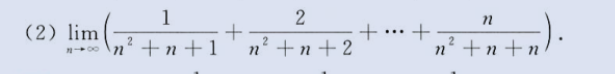 image-20230803165341119
image-20230803165341119
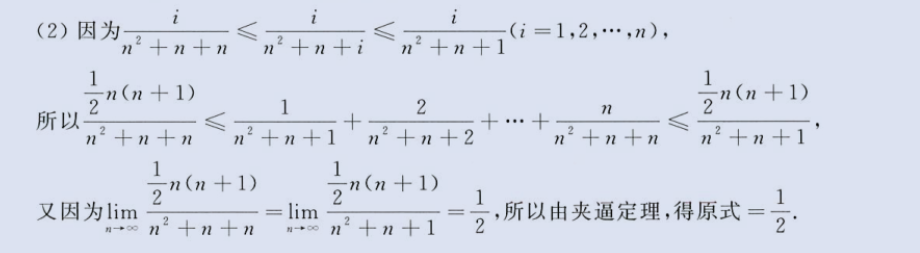 image-20230803165411264
image-20230803165411264
积分定义求极限
1、简单积分定义(注意步长
dx 的选择,加和式子两个相邻自变量x 之差)
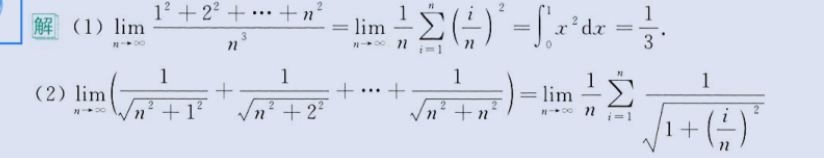 image-20230803165518723
image-20230803165518723
2、放缩+积分
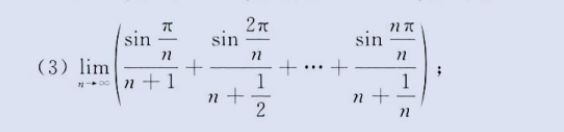 image-20230803165702385
image-20230803165702385
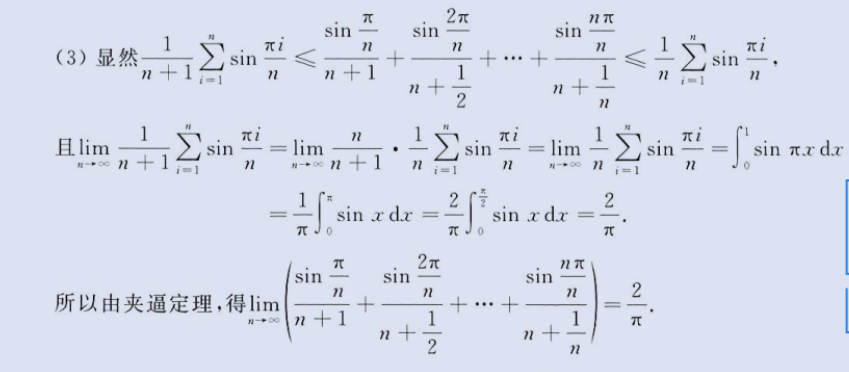 image-20230803165719650
image-20230803165719650
3、积化和(e变换)+积分
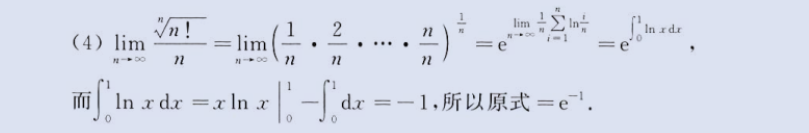 image-20230803170028070
image-20230803170028070
中值定理求极限
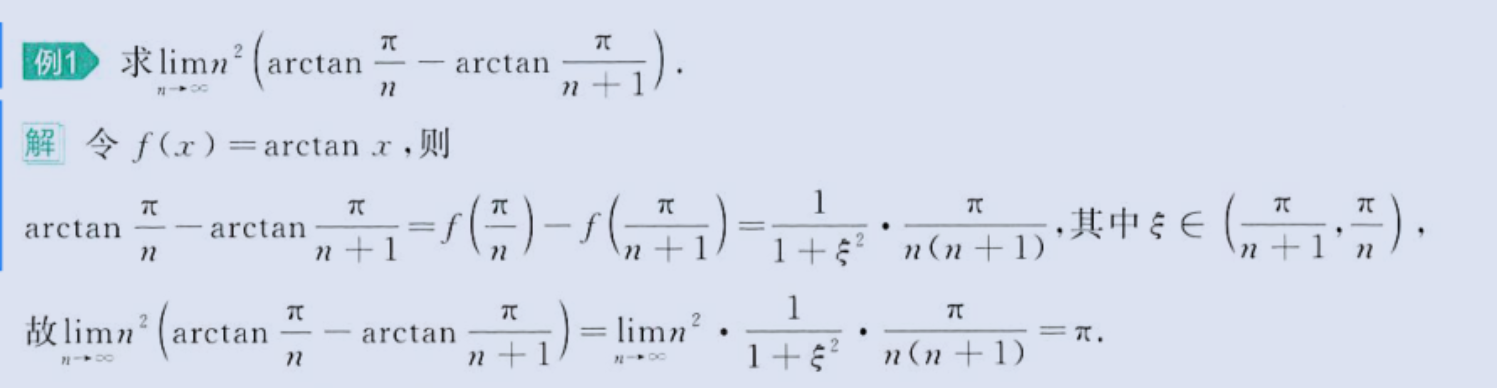 image-20230803181859488
image-20230803181859488
变限
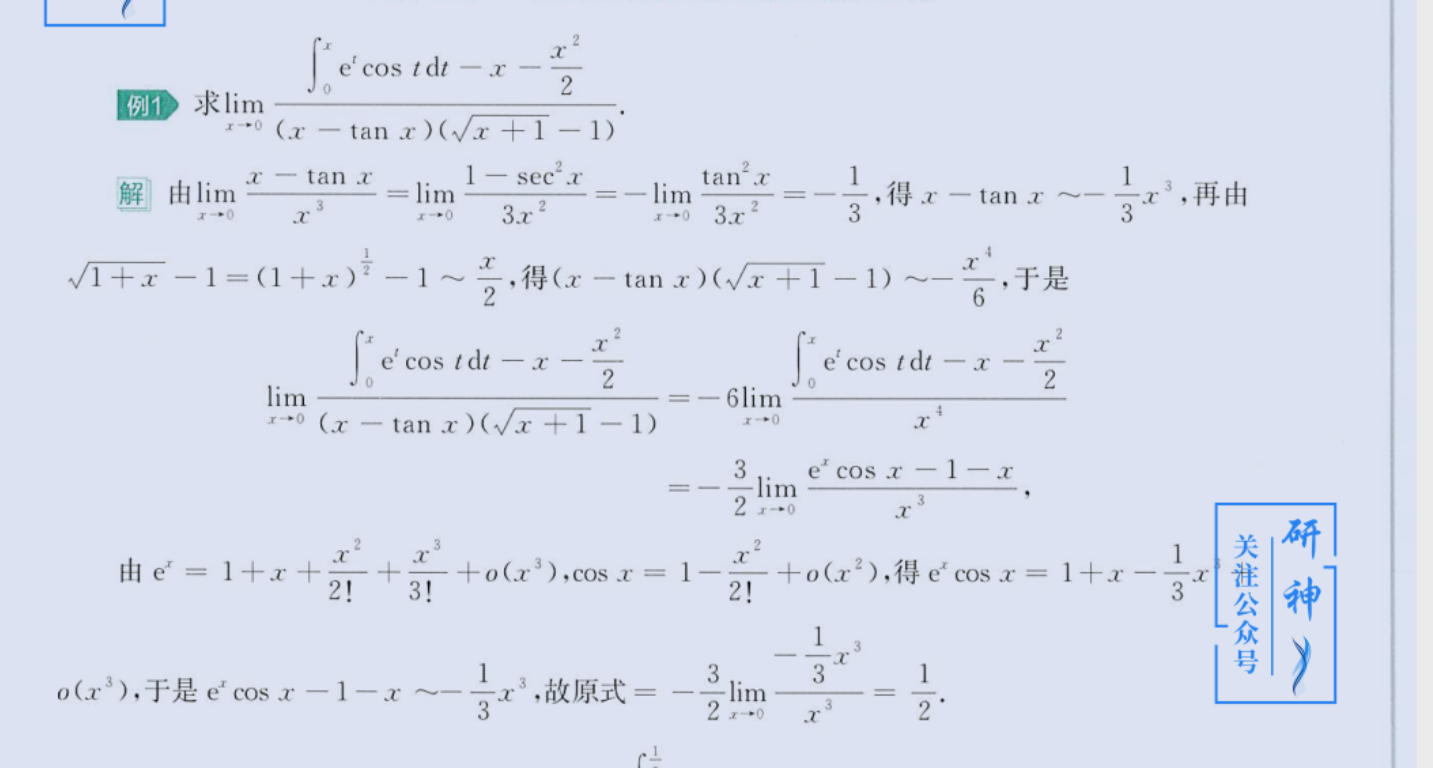 image-20230803182248090
image-20230803182248090
第二章-导数与微分
高数
第二章 导数与微分 (flowus.cn)
知识点
导数概念
 image-20230803221123360
image-20230803221123360
微分概念
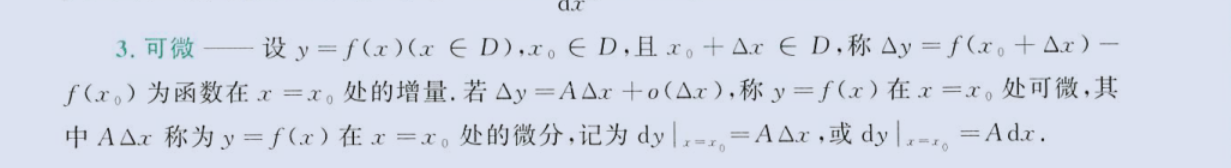 image-20230803221237952
image-20230803221237952
可导与可微关系
一阶等价,高阶可微必可导,可微要求每个偏导存在
常用导数
 image-20230803215943961
image-20230803215943961
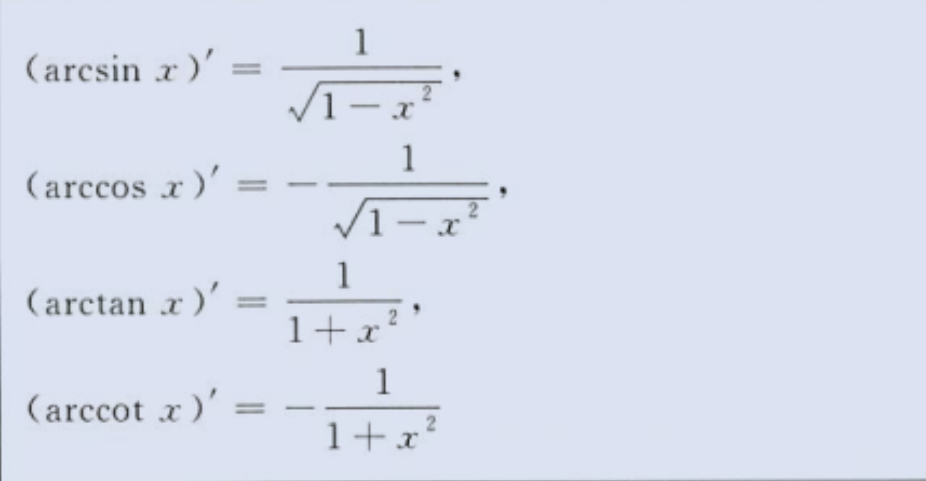 image-20230803220038613
image-20230803220038613
高阶导数
 image-20230803220431466
image-20230803220431466
第7个是牛顿-莱布尼兹公式
复合函数求导
 image-20230803220542621
image-20230803220542621
反函数求导
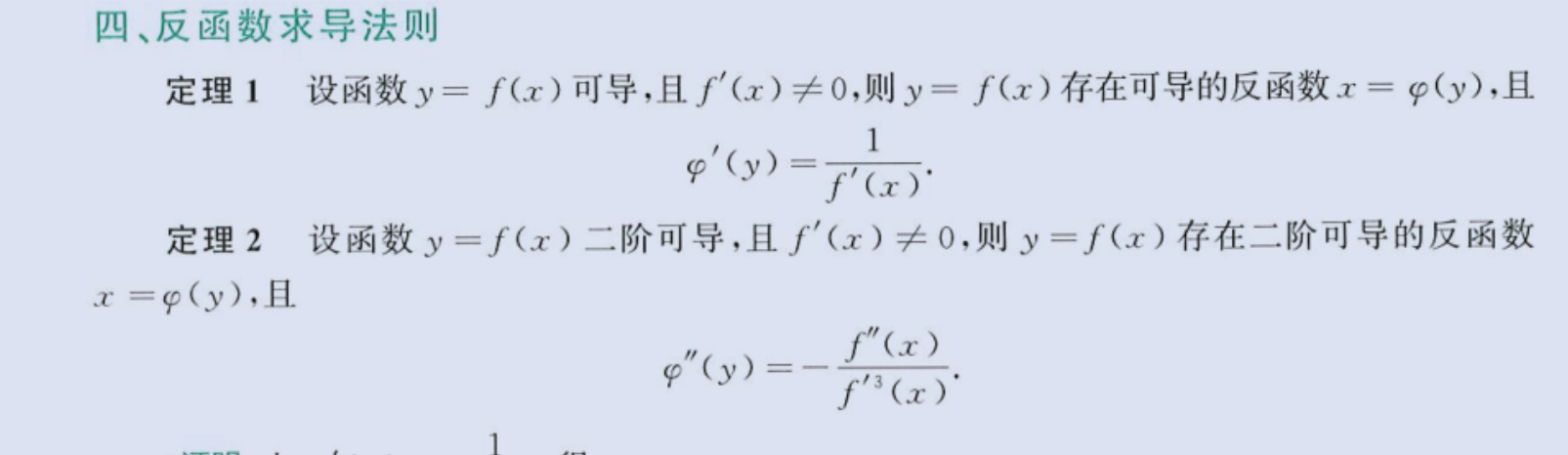 image-20230803220615816
image-20230803220615816
隐函数导数与隐函数存在定理
 image-20230803220836408
image-20230803220836408
参数方程求导
 image-20230803220934900
image-20230803220934900
题型
导数定义、凑定义
1、简单凑定义
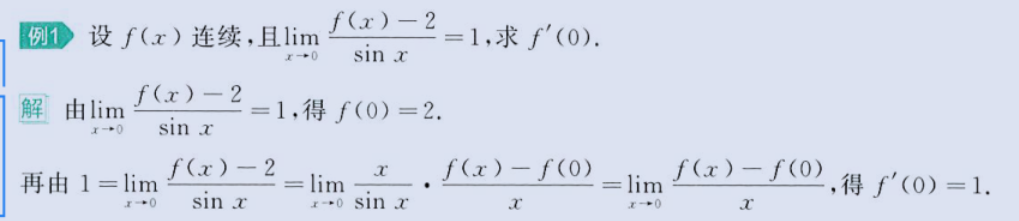 image-20230803221838904
image-20230803221838904
2、保两侧、不能跨、阶相同
 image-20230803222143639
image-20230803222143639
 image-20230803222520102
image-20230803222520102
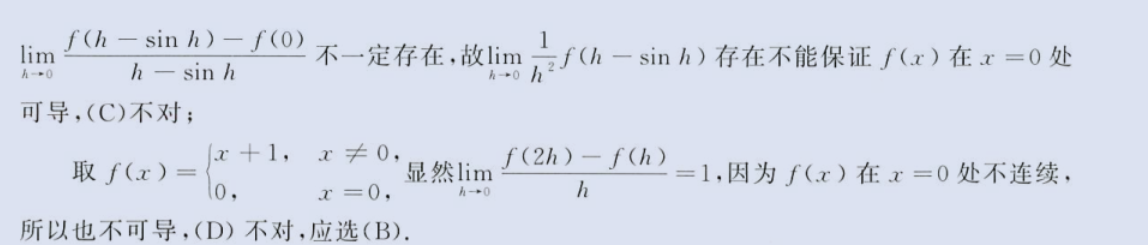 image-20230803222748436
image-20230803222748436
3、保两侧
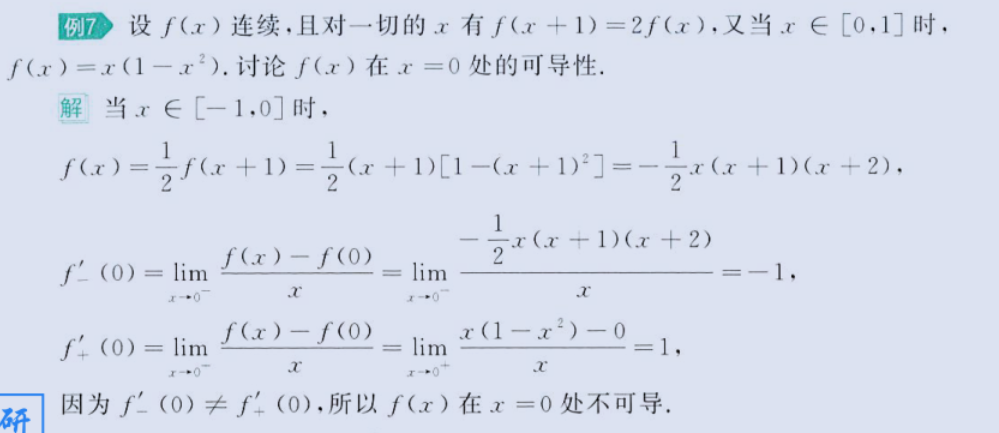
隐函数求导
1、简单对 x 求导
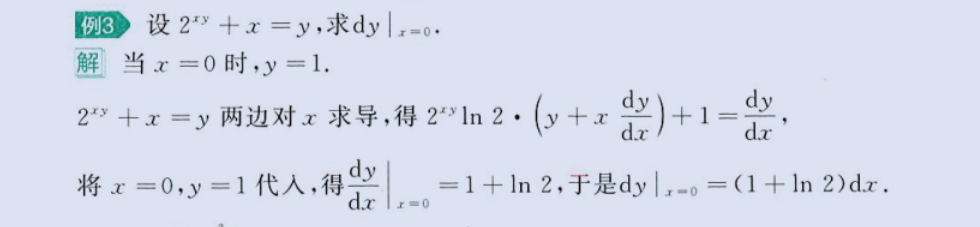 image-20230803223450606
image-20230803223450606
2、结合变上限积分
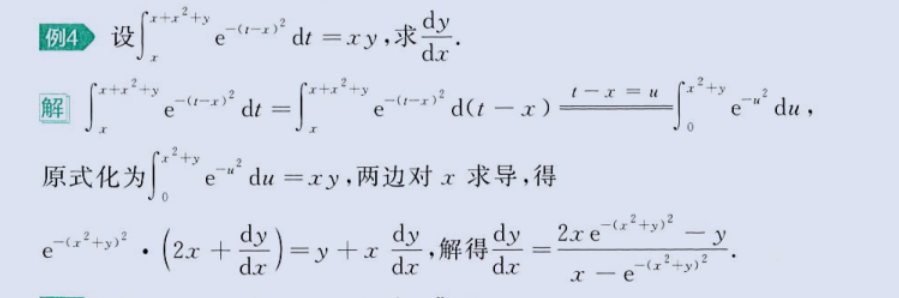 image-20230803223655329
image-20230803223655329
参数方程求导
 image-20230803224118324
image-20230803224118324
高阶导数
 image-20230803224146753
image-20230803224146753
 image-20230803224249436
image-20230803224249436
第三章-一元函数微分学的应用
高数
第三章 一元函数微分学的应用 (flowus.cn)
知识点
罗尔中值定理
 image-20230804093843135
image-20230804093843135
拉格朗日中值定理
 image-20230804093906737
image-20230804093906737
柯西中值定理
 image-20230804094214170
image-20230804094214170
泰勒中值定理
 image-20230804094309860
image-20230804094309860
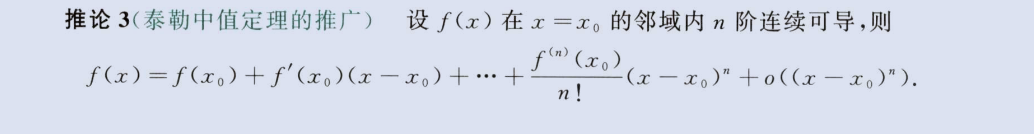 image-20230804095002711
image-20230804095002711
麦克劳林公式

导数零点定理
 image-20230804094715790
image-20230804094715790
导数介值定理
 image-20230804094932182
image-20230804094932182
弧微分
 image-20230804095307798
image-20230804095307798
曲率半径
 image-20230804095355735
image-20230804095355735
积分中值定理
 image-20230804175948502
image-20230804175948502
 image-20230804175920152
image-20230804175920152
题型
证明 n 阶导为0
1、导数介值定理
 image-20230804100724787
image-20230804100724787
2、罗尔定理
 image-20230804100836589
image-20230804100836589
3、拉格朗日中值定理
 image-20230804101259571
image-20230804101259571
证明结论为一个含中值 ξ
的方程 - 辅助函数
1、还原法 (ln型)
 image-20230804101736670
image-20230804101736670
 image-20230804101915902
image-20230804101915902
 image-20230804102244964
image-20230804102244964
 image-20230804103713292
image-20230804103713292
2、分组构造 (e型)
 image-20230804103004508
image-20230804103004508
看不出来可以考虑待定系数 e^kx [af(x)+bf'(x)]
 image-20230804103853668
image-20230804103853668
 image-20230804104507575
image-20230804104507575
3、凑微(移项)
 image-20230804104851572
image-20230804104851572
证明结论含 中值 ξ、a、b
1、a、b 与 ξ 可分离
 image-20230804105253013
image-20230804105253013
a、b、ξ 写成一个原函数
 image-20230804105330189
image-20230804105330189
a 、b 与 ξ 分离构造柯西
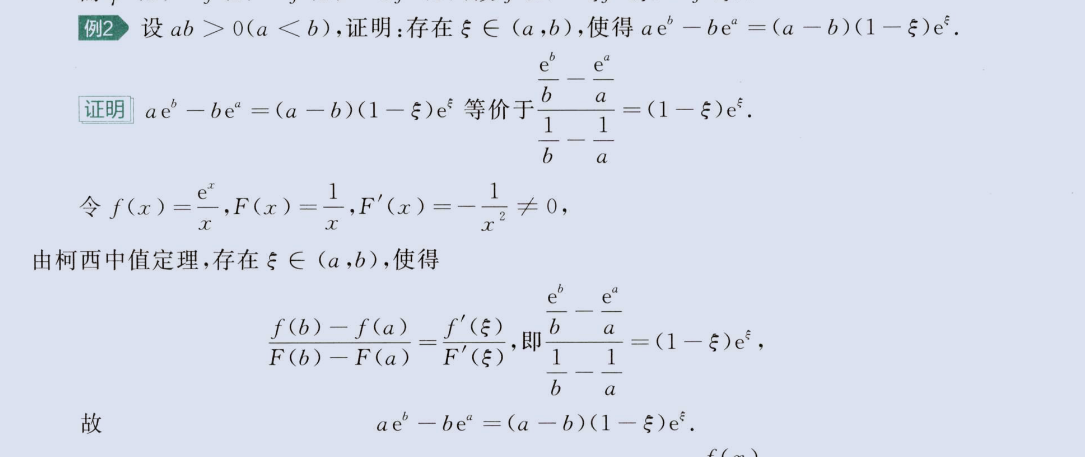 image-20230804110110276
image-20230804110110276
2、a 、b 与 ξ 不可分离
(凑微移项 ,ξ 换成 x)
 image-20230804110243311
image-20230804110243311
 image-20230804110517025
image-20230804110517025
 image-20230804110638903
image-20230804110638903
结论中含两个或以上中值
1、只含中值的导数
 image-20230804110736392
image-20230804110736392
 image-20230804110903232
image-20230804110903232
 image-20230804111134645
image-20230804111134645
2、两个中值项复杂度不同
 image-20230804111538535
image-20230804111538535
两次拉格朗日
 image-20230804111550943
image-20230804111550943
柯西+拉格朗日(柯西移项配凑拉格朗日)
 image-20230804111753235
image-20230804111753235
 3、结论中含两个中值 ξ 和
η,且对应项完全相等
3、结论中含两个中值 ξ 和
η,且对应项完全相等
 image-20230804172414293
image-20230804172414293
 image-20230804172442124
image-20230804172442124
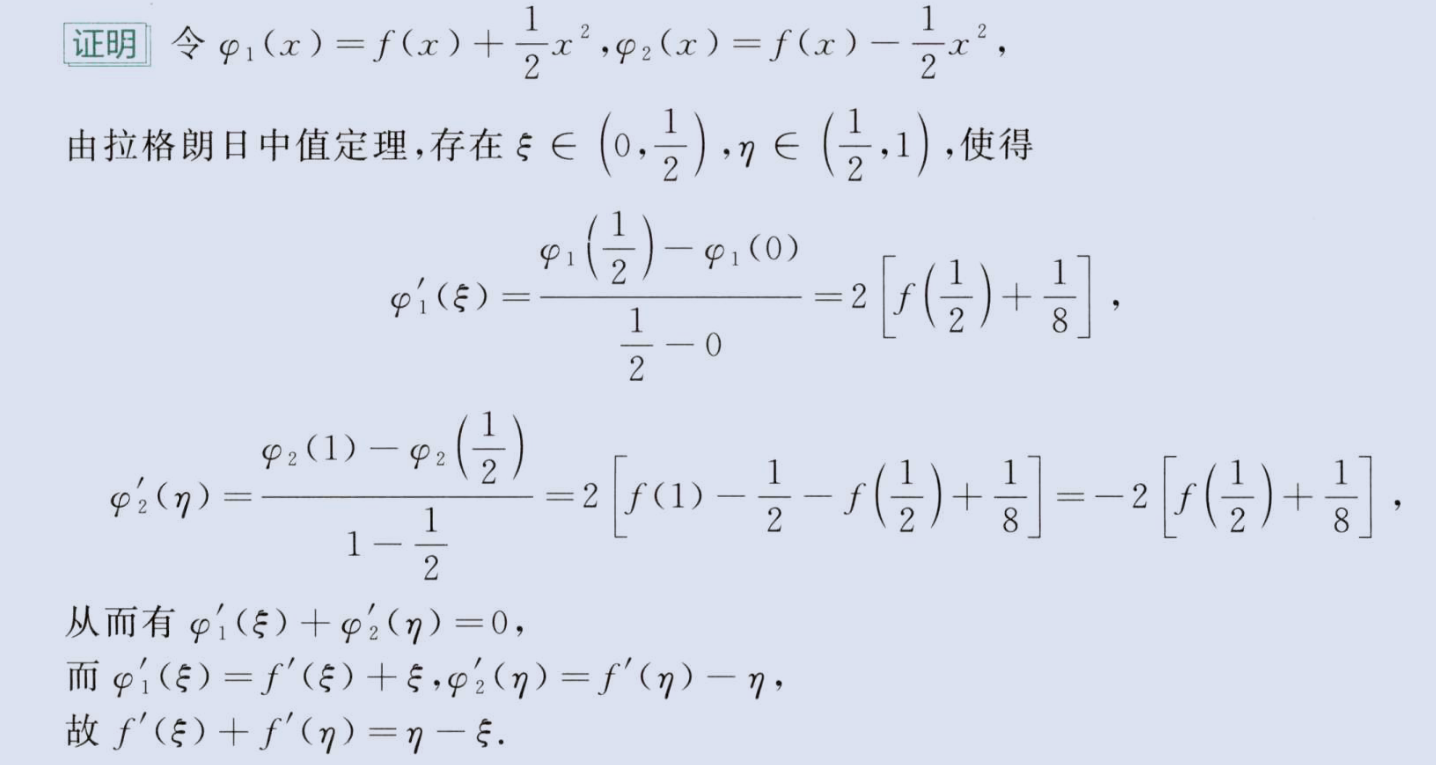 image-20230804172505249
image-20230804172505249
中值定理中的 θ
1、泰勒中值定理
 image-20230804173054665
image-20230804173054665
2、推广的积分中值定理
 image-20230804175602141
image-20230804175602141
拉格朗日常规
 image-20230804181646070
image-20230804181646070
 image-20230804181636957
image-20230804181636957
泰勒中值定理常规
1、相同点展开
 image-20230804181025816
image-20230804181025816
2、不同点展开
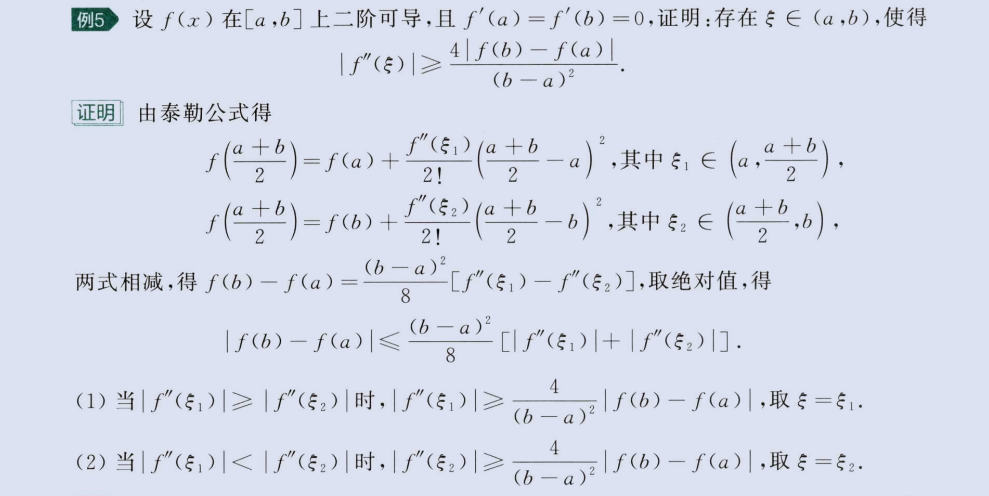 image-20230804181401262
image-20230804181401262
二阶导保号性 +
中值定理(实际上是导数单调性问题)
 image-20230804182512202
image-20230804182512202
1、 与拉格朗日
 image-20230804182654479
image-20230804182654479
2、与泰勒中值定理
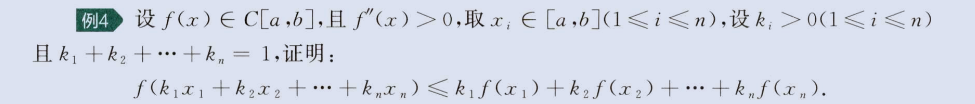 image-20230804182755308
image-20230804182755308
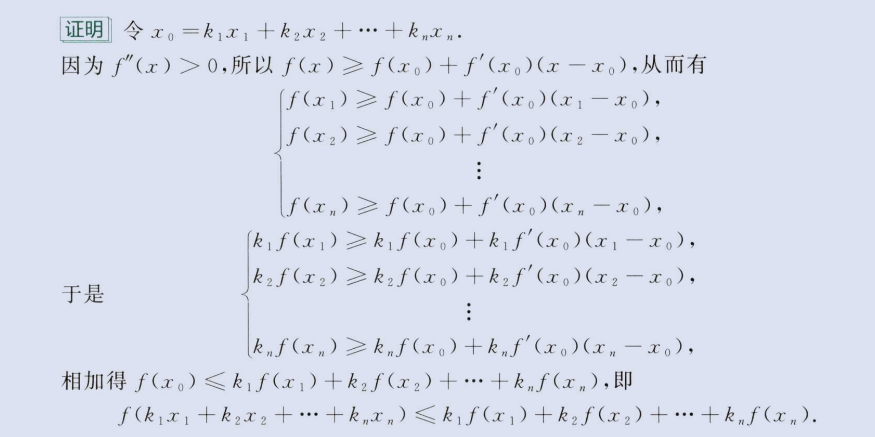 image-20230804182419183
image-20230804182419183
不等式证明与中值定理、凹凸性
1、与拉格朗日
 image-20230804183121631
image-20230804183121631
2、与柯西中值定理
 image-20230804183313477
image-20230804183313477
3、与凹凸性
 image-20230804183436383
image-20230804183436383
函数零点与方程的根
 image-20230804215030303
image-20230804215030303
原函数与罗尔定理
 image-20230804215153533
image-20230804215153533
拉格朗日中值定理与放缩
 image-20230804215852617
image-20230804215852617
第四章-不定积分
高数
第四章 不定积分 (flowus.cn)
知识点
不定积分基本公式
 image-20230805143634466
image-20230805143634466
第一类换元积分(凑微分)
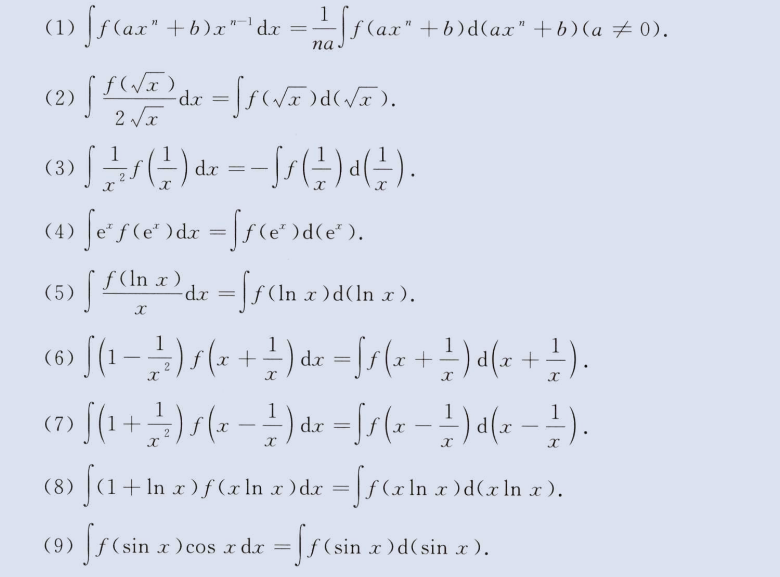 image-20230805164012976
image-20230805164012976
 image-20230805164028561
image-20230805164028561
第二类换元积分
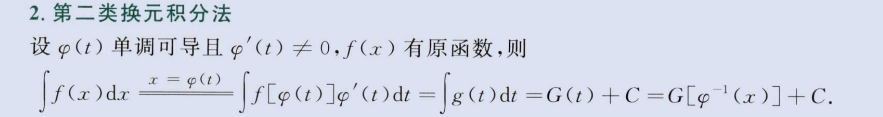 image-20230805164207134
image-20230805164207134
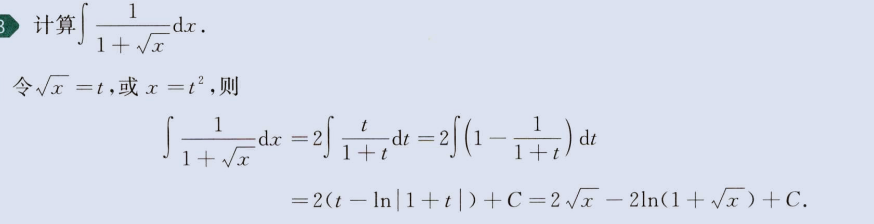 image-20230805164311511
image-20230805164311511
分部积分
 image-20230805144318520
image-20230805144318520
三角有理函数积分与万能公式
 image-20230805163403838
image-20230805163403838
题型
换元积分
1、凑微分
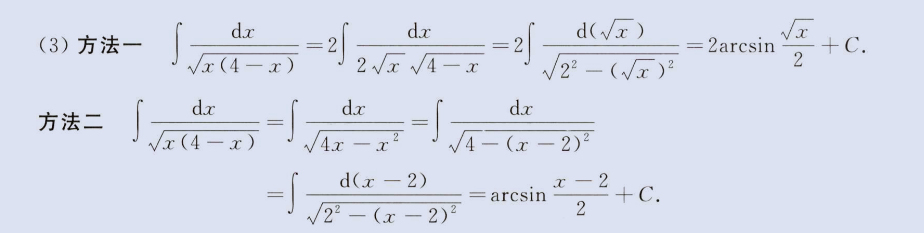 image-20230805164614862
image-20230805164614862
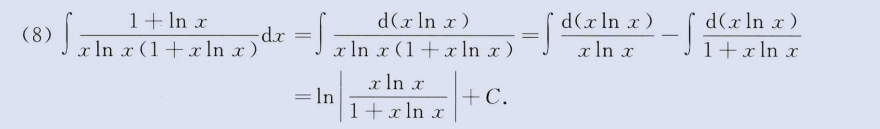 image-20230805164943634
image-20230805164943634
注意ln的定义域绝对值
2、第二类换元积分
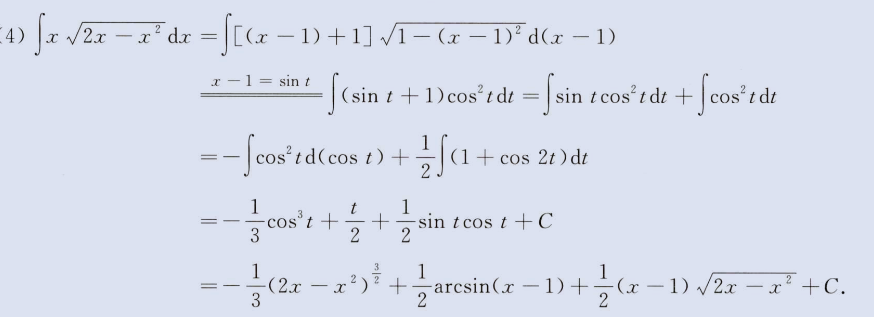 image-20230805165129076
image-20230805165129076
分部积分
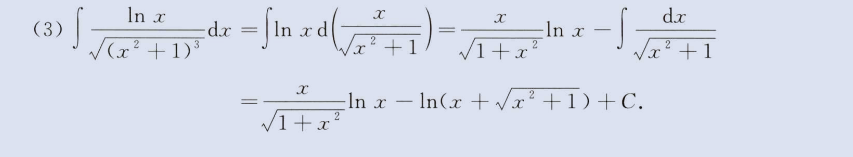 image-20230805165744200
image-20230805165744200
 image-20230805171902636
image-20230805171902636
三角函数积分
1、tan(x)导数1/cos^2(x),tan(x/2)导数1/(1+cos(x))
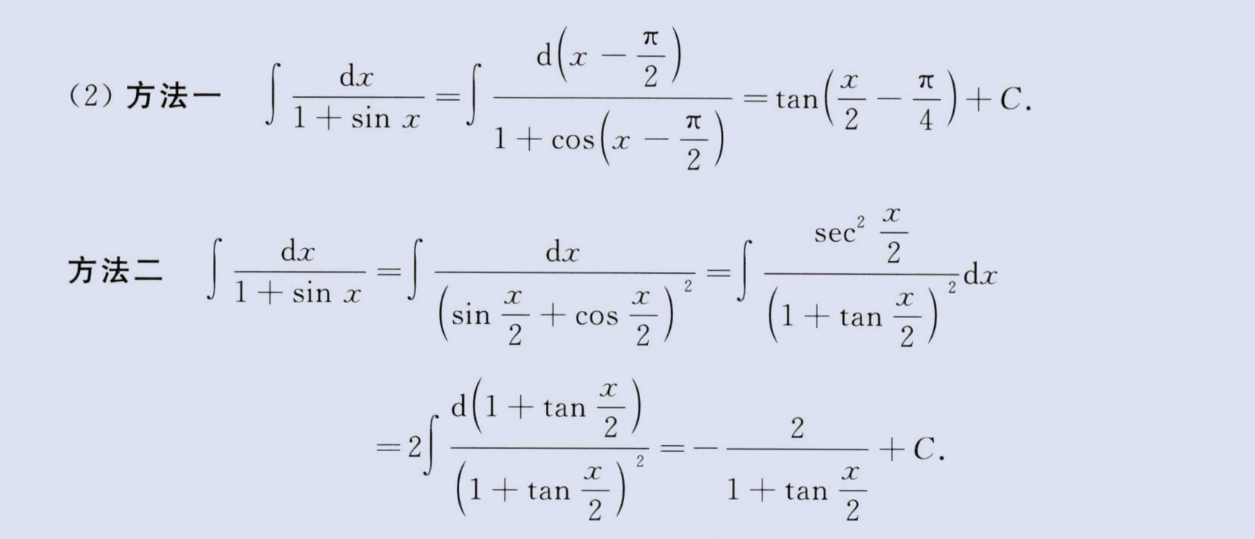 image-20230805172720597
image-20230805172720597
 image-20230805172808408
image-20230805172808408
2、分子分母都是一次考虑进行系数配凑导数与原函数
 image-20230805173527229
image-20230805173527229
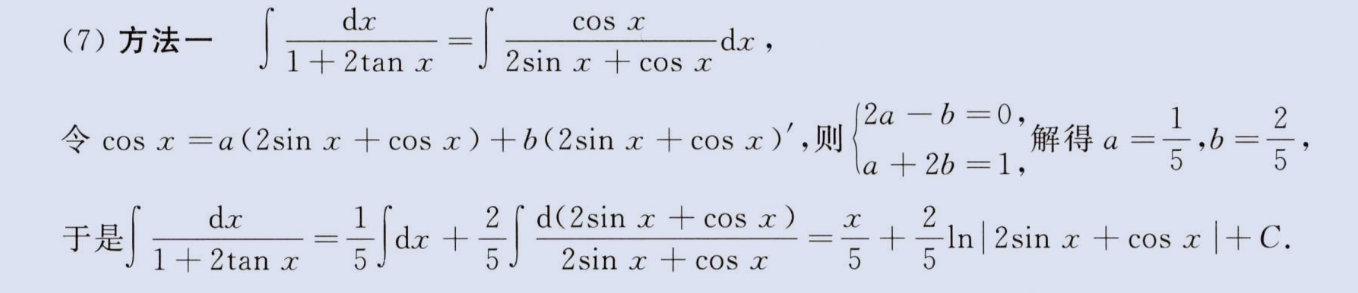 image-20230805173130490
image-20230805173130490
3、倍角(sin2x的原函数具有平方)
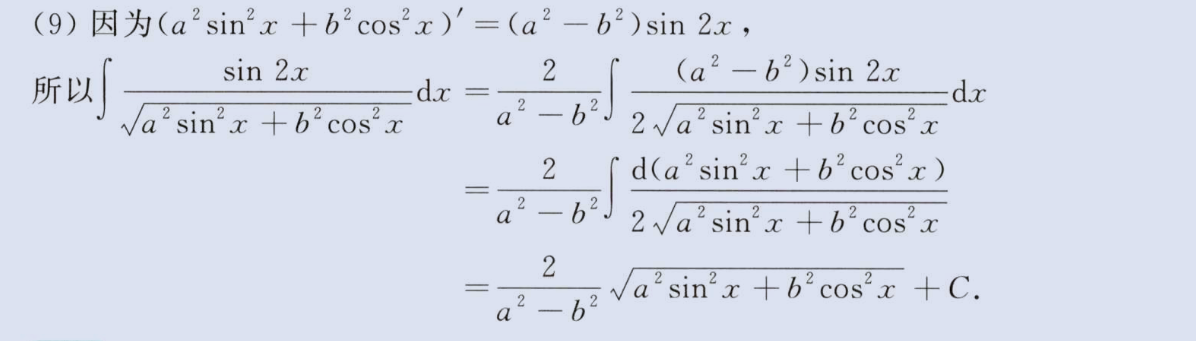 image-20230805173936978
image-20230805173936978
第五章-定积分及其应用
高数
第五章 定积分 (flowus.cn)
知识点
定积分定义
 image-20230806135657839
image-20230806135657839
积分中值定理
介值定理推导,闭区间
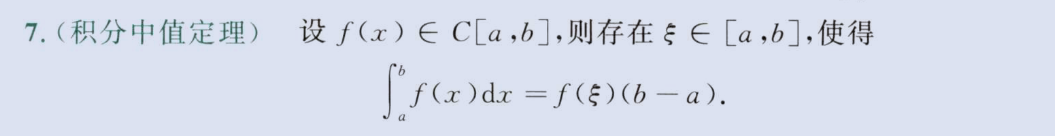 image-20230806141052742
image-20230806141052742
推广的积分中值定理
拉格朗日推导,开区间
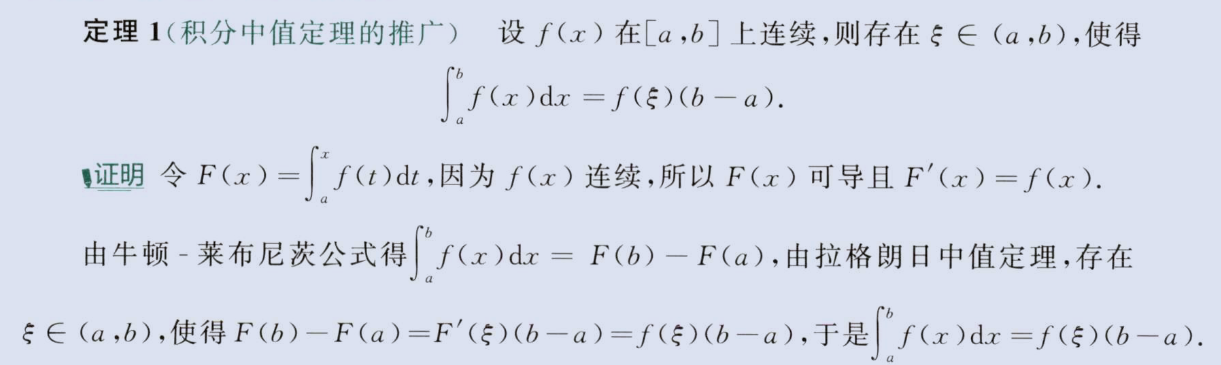 image-20230806141244834
image-20230806141244834
积分第一中值定理
介值定理推导,闭区间

积分柯西不等式
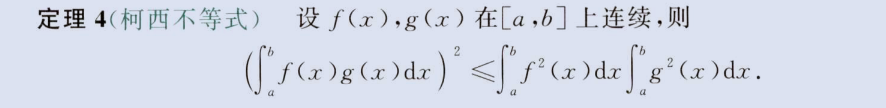 image-20230806141547750
image-20230806141547750
三角函数定积分
注意第(3)点,换元 (Π-x)=u 证明

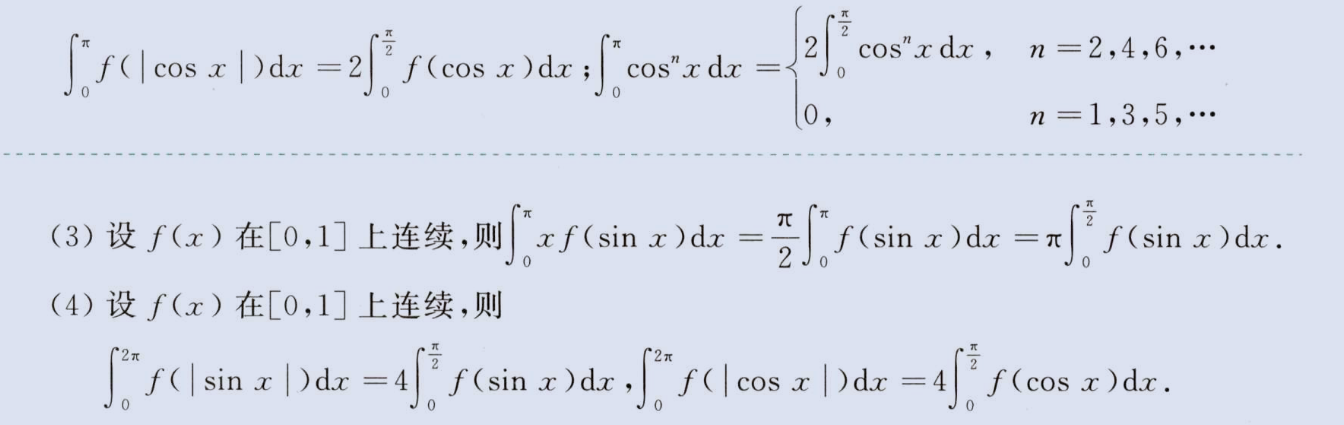 image-20230806142401472
image-20230806142401472
广义积分敛散性(积分区间无限)
 image-20230806151452465
image-20230806151452465
 image-20230806151505030
image-20230806151505030
 image-20230806151532587
image-20230806151532587
注意定义3,区间左右无穷,左右都要收敛才能收敛,如下
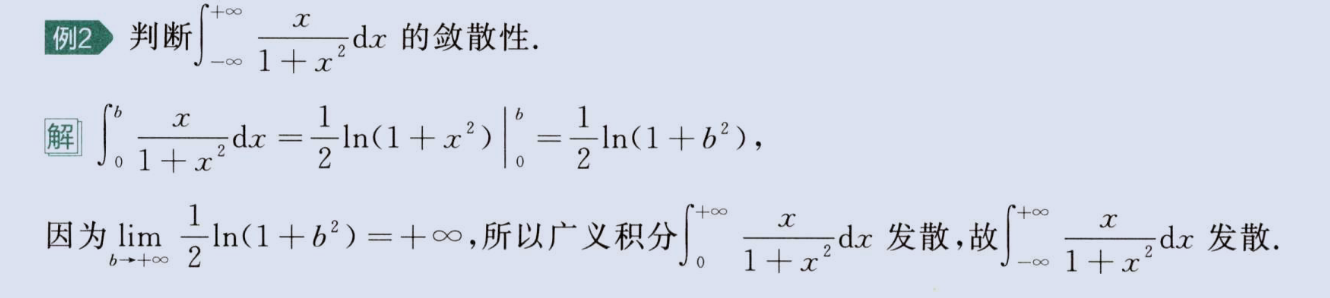 image-20230806151613740
image-20230806151613740
广义积分敛散性(积分区间有限)
第二类间断点在端点
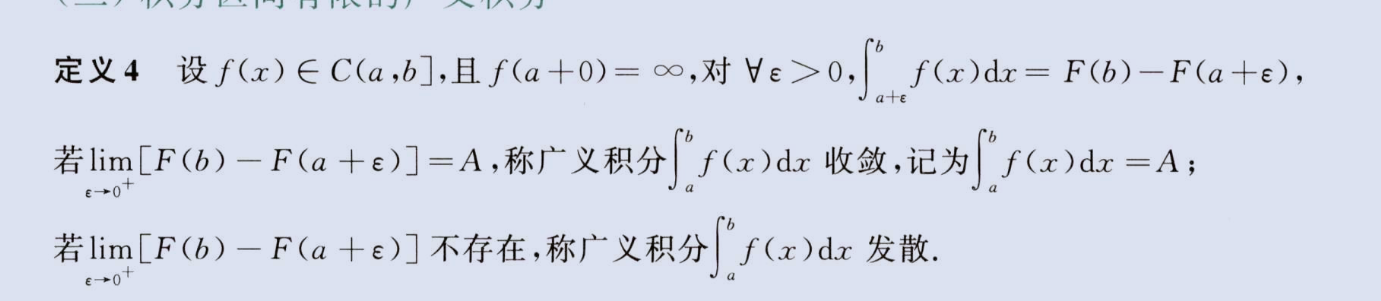 image-20230806152242258
image-20230806152242258
第二类间断点在中间
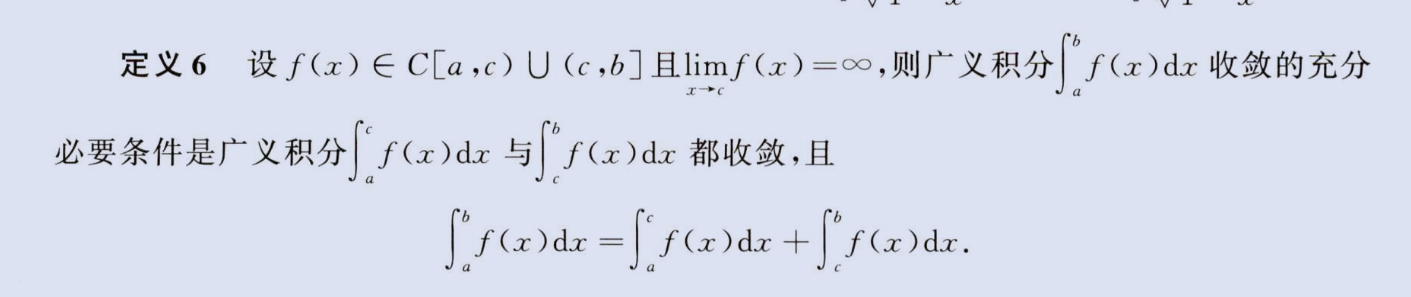 image-20230806152421410
image-20230806152421410
广义积分敛散性判别法
1、左无穷、右无穷区间(幂次大于1 收敛)
注意a 和 阿尔法 字母,幂是 阿尔法
 image-20230806152858187
image-20230806152858187
2、左无穷、右无穷间断点(幂次小于 1 收敛)
 image-20230806153423810
image-20230806153423810
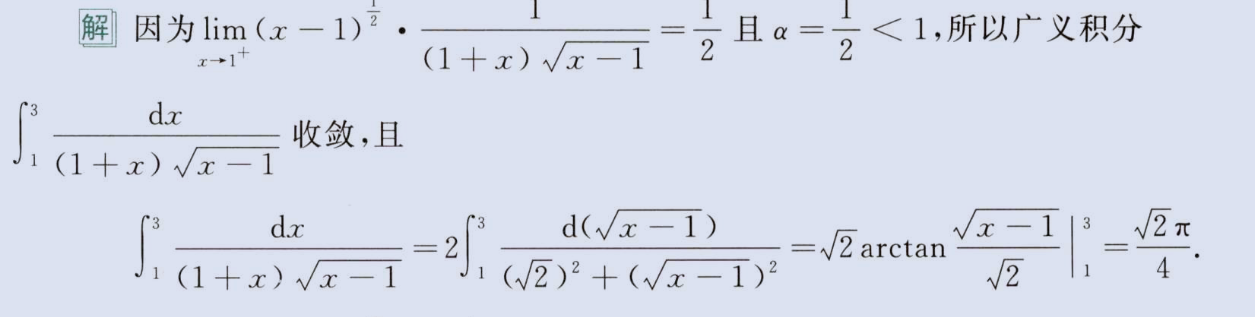 image-20230806153742013
image-20230806153742013
3、一边无穷区间,一边无穷间断点
 image-20230806153859994
image-20230806153859994
4、放缩证明敛散性
 image-20230806154041608
image-20230806154041608
常见的一个反常积分 ┏ 函数
 image-20230806154153895
image-20230806154153895
定积分与面积
0、曲线长度(弧微分)

1、直角坐标
2、极坐标
 image-20230806154437570
image-20230806154437570
面积微分是三角形底×高
3、旋转曲面与参数方程
 image-20230806154646560
image-20230806154646560
面积微分是圆环带,圆环周长×弧微分
定积分与体积
总结:计算截面积,堆砌
 image-20230806155416666
image-20230806155416666
题型
定积分加和定义
1、乘积型转化e
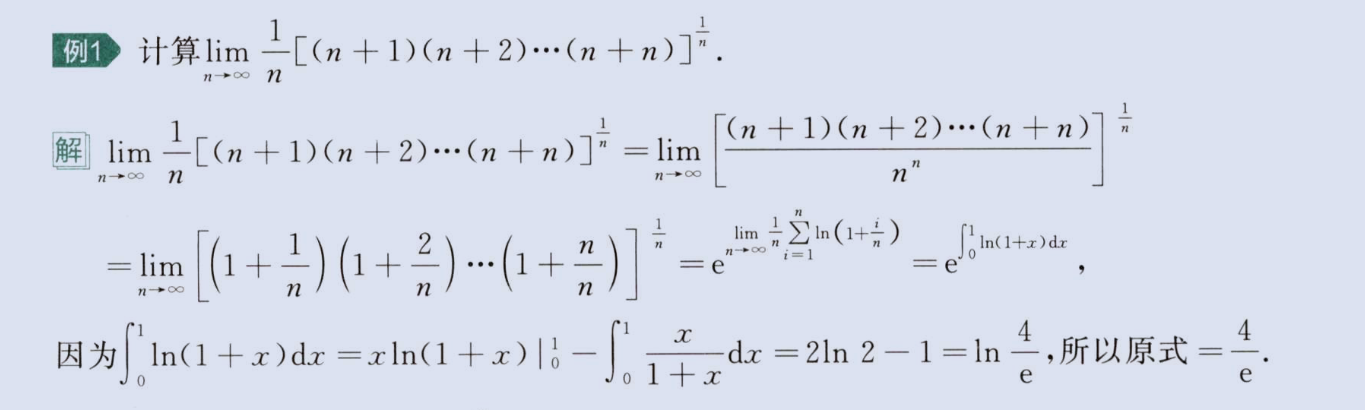 image-20230806155607289
image-20230806155607289
2、夹逼定理与积分定义
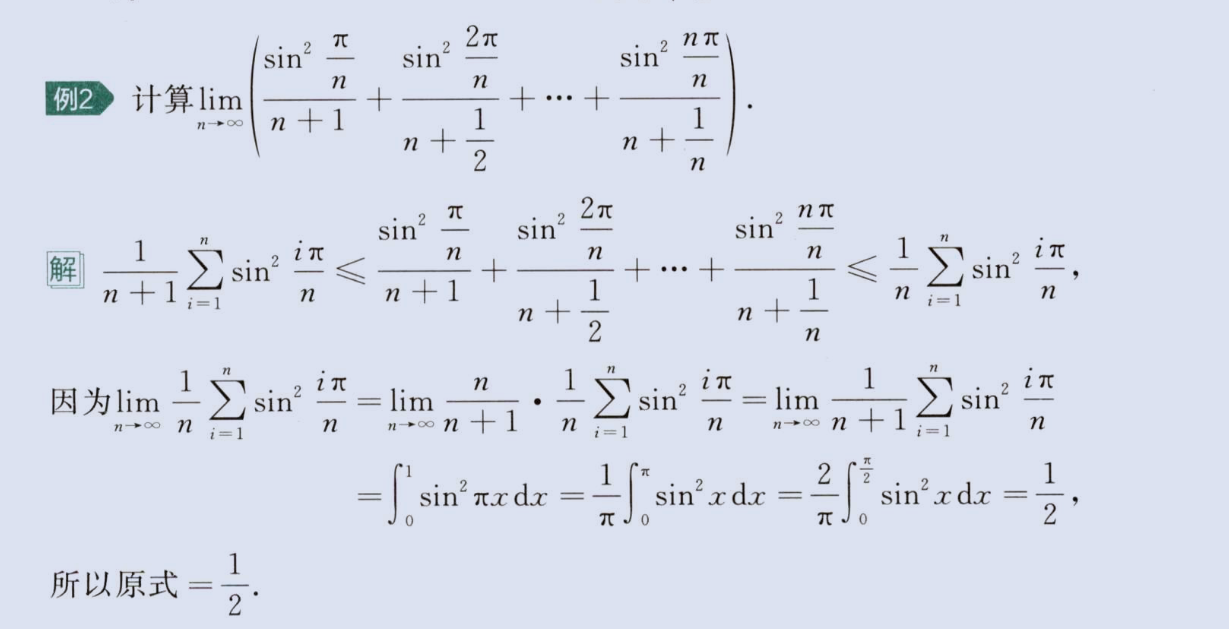 image-20230806155737604
image-20230806155737604
不好算的积分与迭代(假设已经计算出来,再凑出一个)
 image-20230806160129274
image-20230806160129274
变限
1、换元统一变量
 image-20230806160312191
image-20230806160312191
2、与微分方程 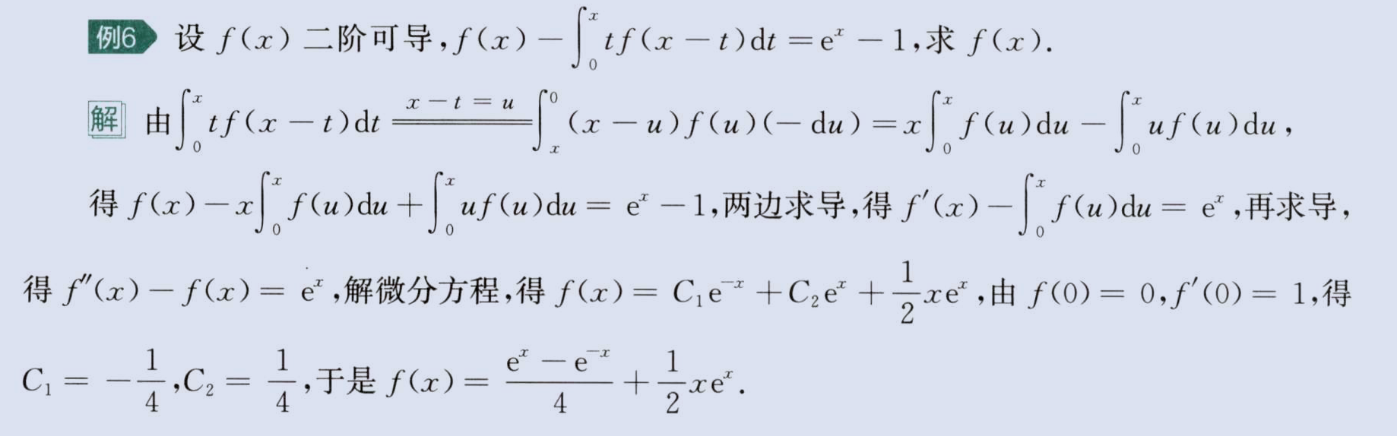
3、与二重积分
 image-20230806160711146
image-20230806160711146
4、凑三角
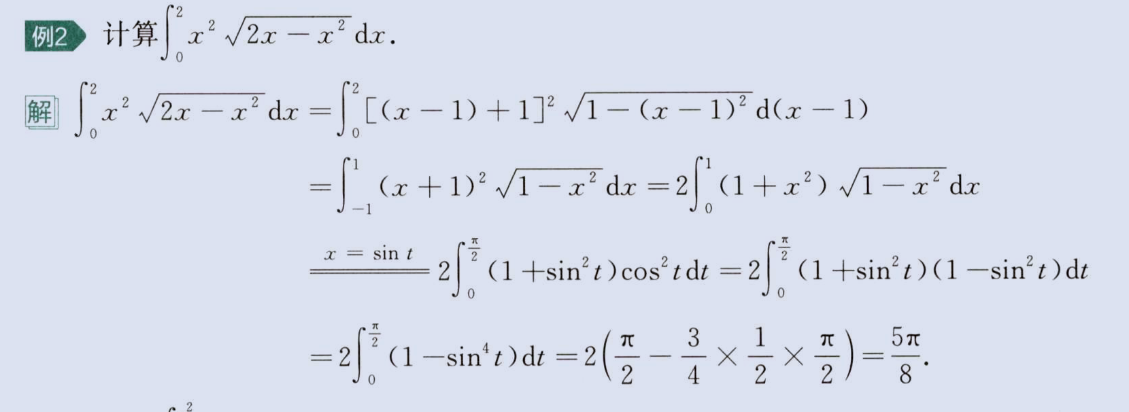 image-20230806160829864
image-20230806160829864
三角轮换(sinx与cosx
,tanx与cotx 转换)
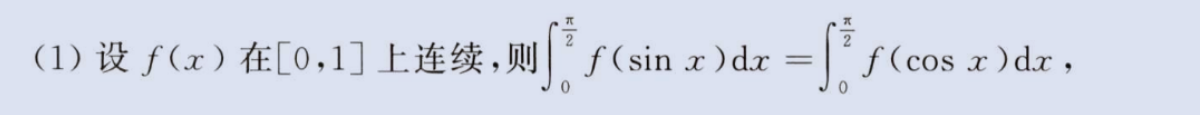 image-20230806161218588
image-20230806161218588
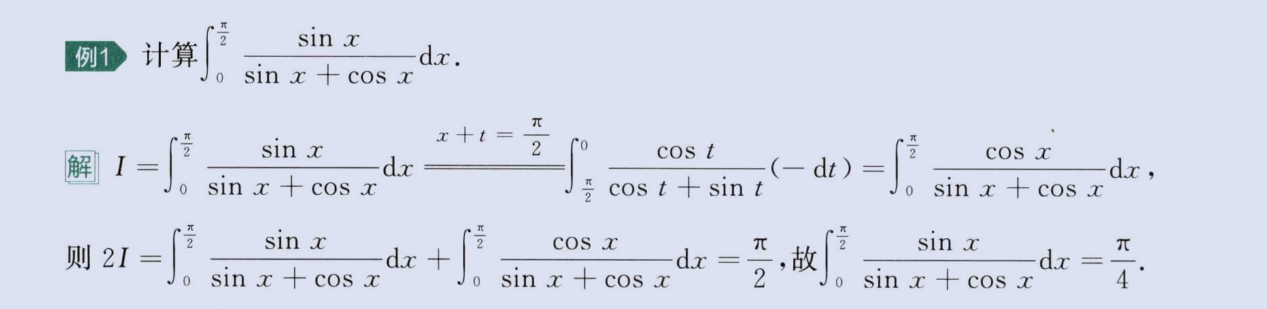 image-20230806161138568
image-20230806161138568
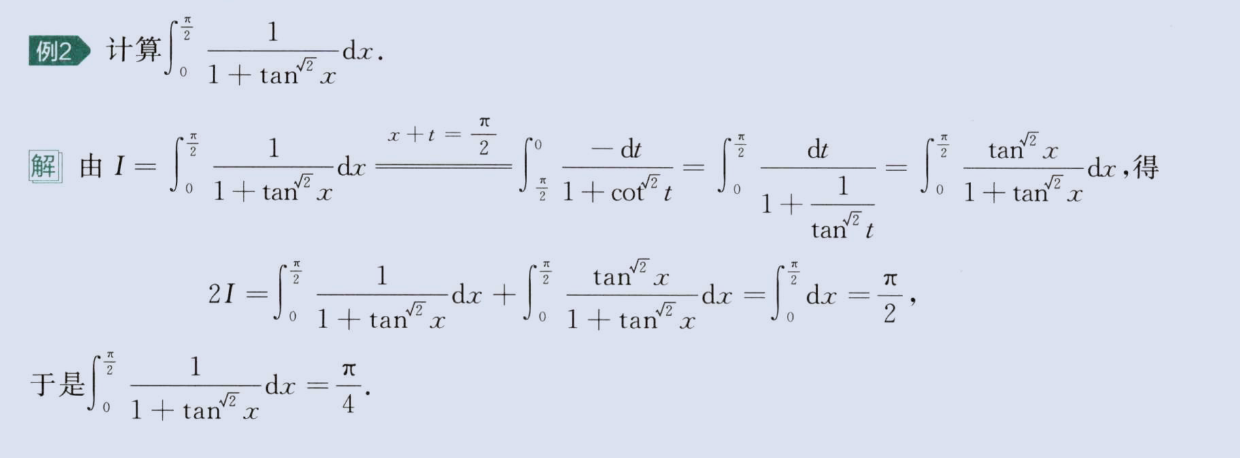 image-20230806161529250
image-20230806161529250
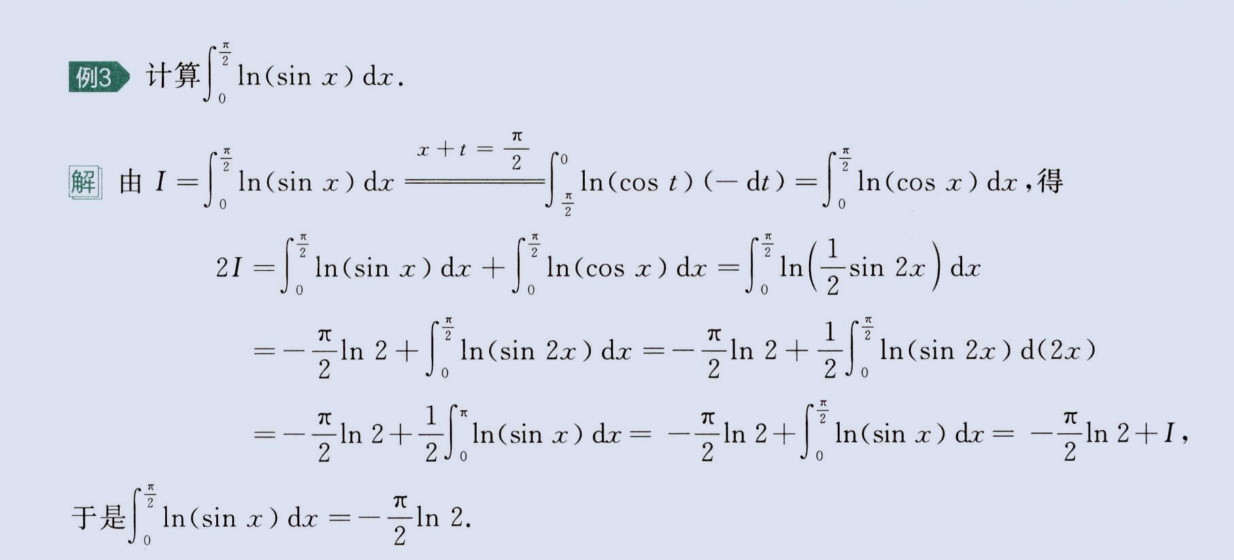 image-20230806161659560
image-20230806161659560
分部积分
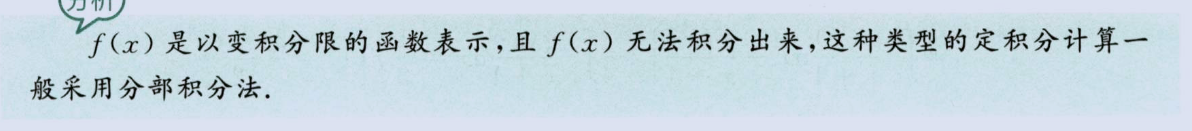 image-20230806161801354
image-20230806161801354
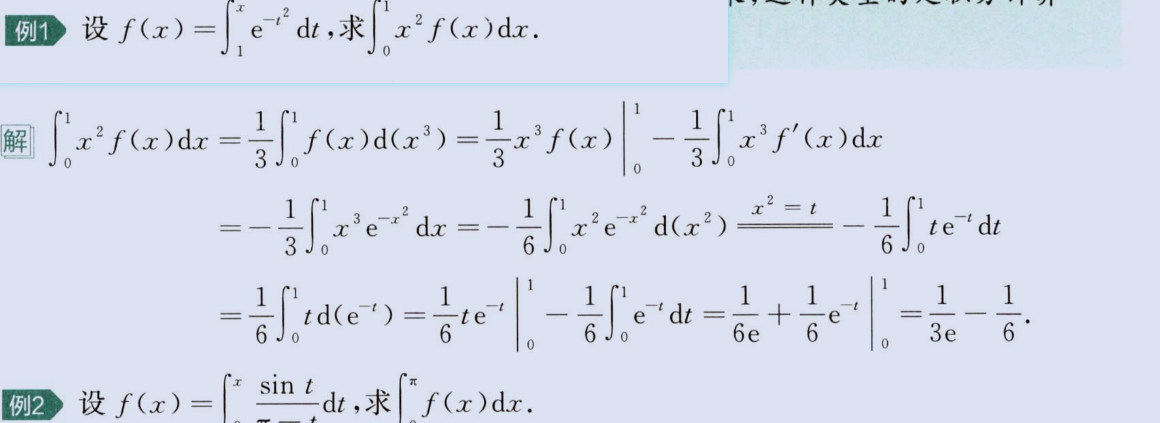 image-20230806161859724
image-20230806161859724
证明题
 image-20230806162534642
image-20230806162534642
证明题 1-连续函数
a、区间变换
 image-20230806162745744
image-20230806162745744
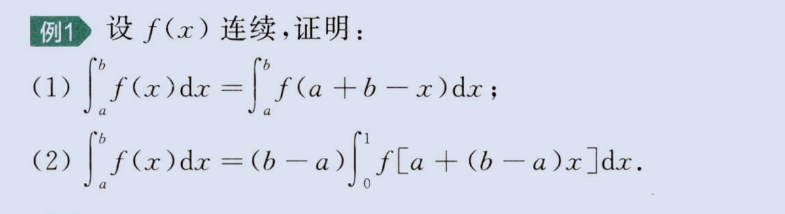
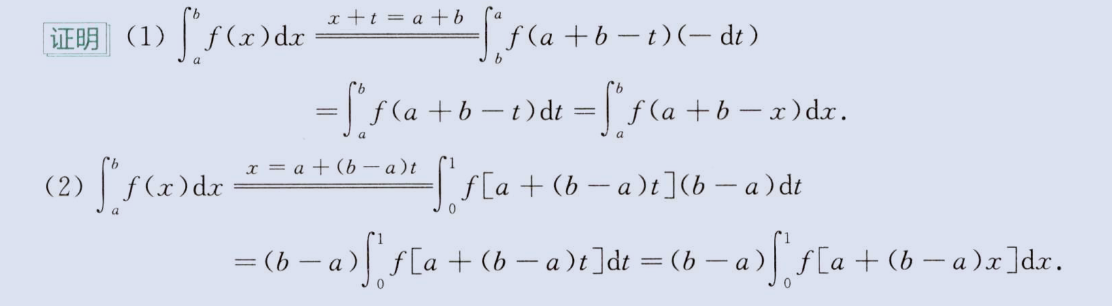 image-20230806162800098
image-20230806162800098
b、统一定积分
 image-20230806163123766
image-20230806163123766
 image-20230806163210136
image-20230806163210136
c、与基本不等式
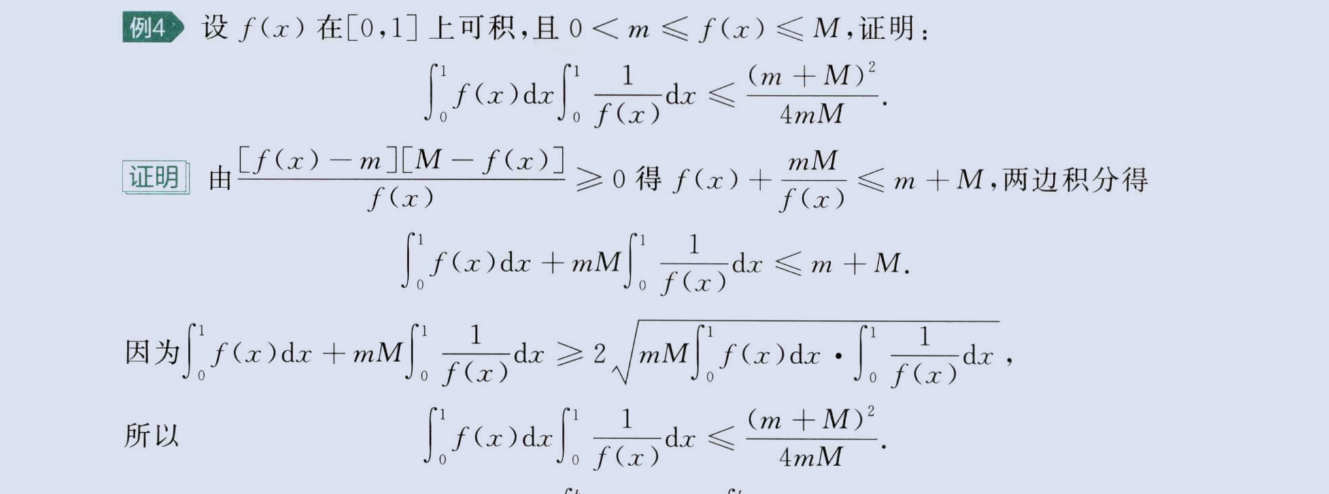 image-20230806163846215
image-20230806163846215
d、零点问题与罗尔定理
 image-20230806164048287
image-20230806164048287
证明题 2 -连续区间+单调性

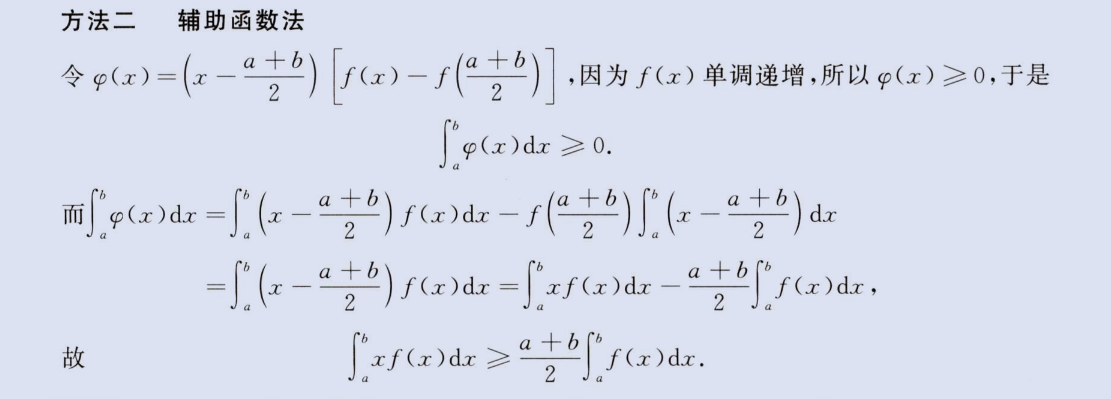 image-20230807152427165
image-20230807152427165
上面方法二利用了x-(a+b)/2积分,两个平方差公式,积出来刚好为0
 image-20230807152811332
image-20230807152811332
上面方法二利用积分区间分割与积分中值定理配凑出(1-a)的公因式
证明题 3 -周期函数(平移性质)
 image-20230807153204985
image-20230807153204985
 image-20230807153331661
image-20230807153331661
证明题 4 -连续可导
 image-20230807153539623
image-20230807153539623
a、拉格朗日
 image-20230807153551952
image-20230807153551952
 image-20230807153726774
image-20230807153726774
b、牛顿-莱布尼兹公式(反向应用)
 image-20230807153850685
image-20230807153850685
c、积分中值定理+牛顿-莱布尼兹(同一个中值x0的应用)
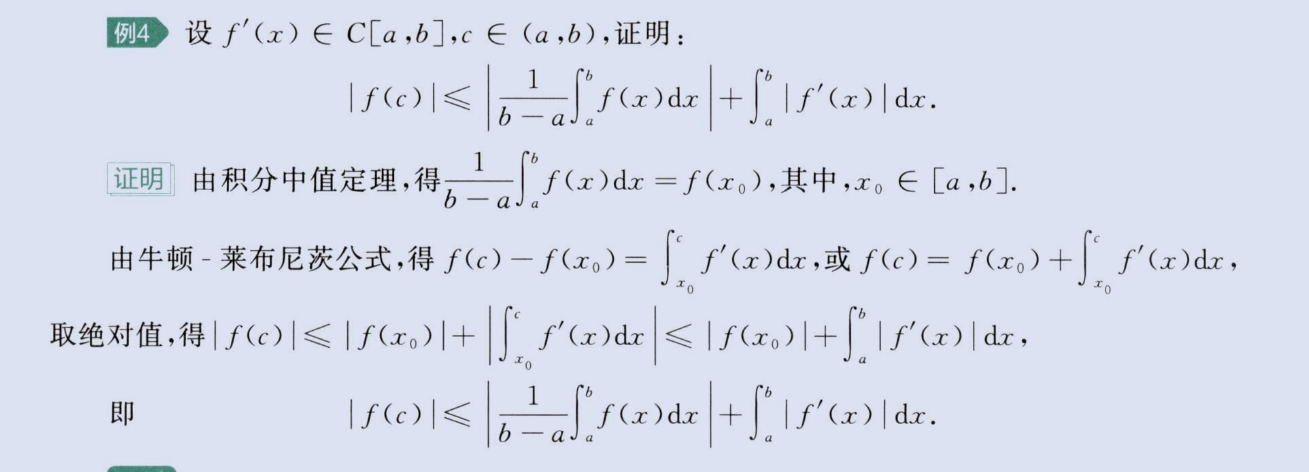 image-20230807154118439
image-20230807154118439
d、积分中值定理+罗尔定理
 image-20230807154642751
image-20230807154642751
e、积分中值定理+拉格朗日
 image-20230807154912995
image-20230807154912995
证明题 5 -高阶导数
 image-20230807155059408
image-20230807155059408
a、F(x)泰勒展开+牛莱公式
 image-20230807155124368
image-20230807155124368
b、f(x)泰勒展开
 image-20230807155527887
image-20230807155527887
c、f(x)泰勒展开+单调性(最后一项的正负问题、从而进行放缩)
 image-20230807155616450
image-20230807155616450
广义积分
分段积分,从间断点断开
 image-20230807160103988
image-20230807160103988
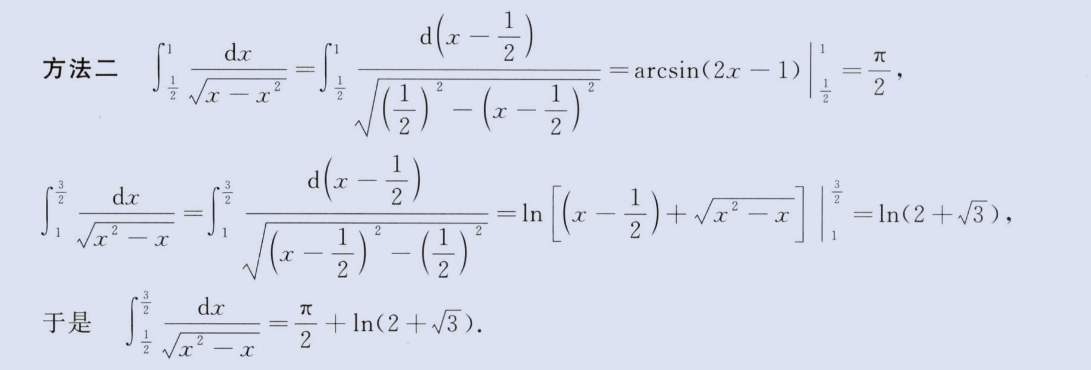 image-20230807160124556
image-20230807160124556
定积分应用
 image-20230807160407318
image-20230807160407318
第六章-多元函数微分学
[高数 第六章 多元函数微分学 (flowus.cn)
知识点
多元函数极限
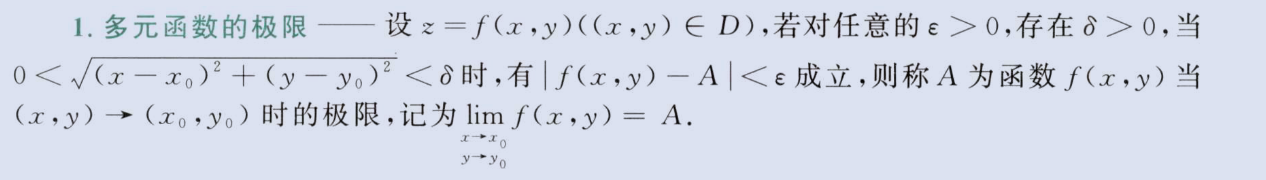 image-20230811200712425
image-20230811200712425
多元函数连续
 image-20230811201035725
image-20230811201035725
偏导
 image-20230811201423864
image-20230811201423864
高阶偏导
 image-20230811201511555
image-20230811201511555
全微
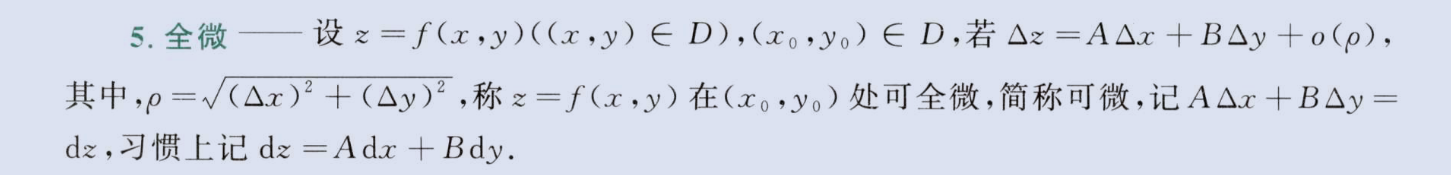 image-20230811201708533
image-20230811201708533
 image-20230811201745517
image-20230811201745517
题型
多元函数极限
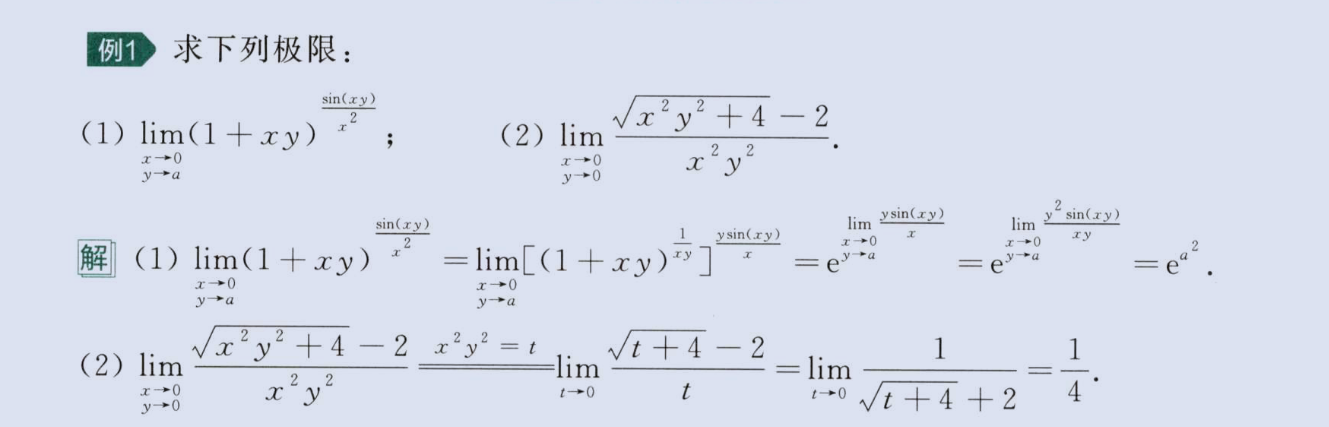 image-20230811204533335
image-20230811204533335
连续、可微、可偏导性
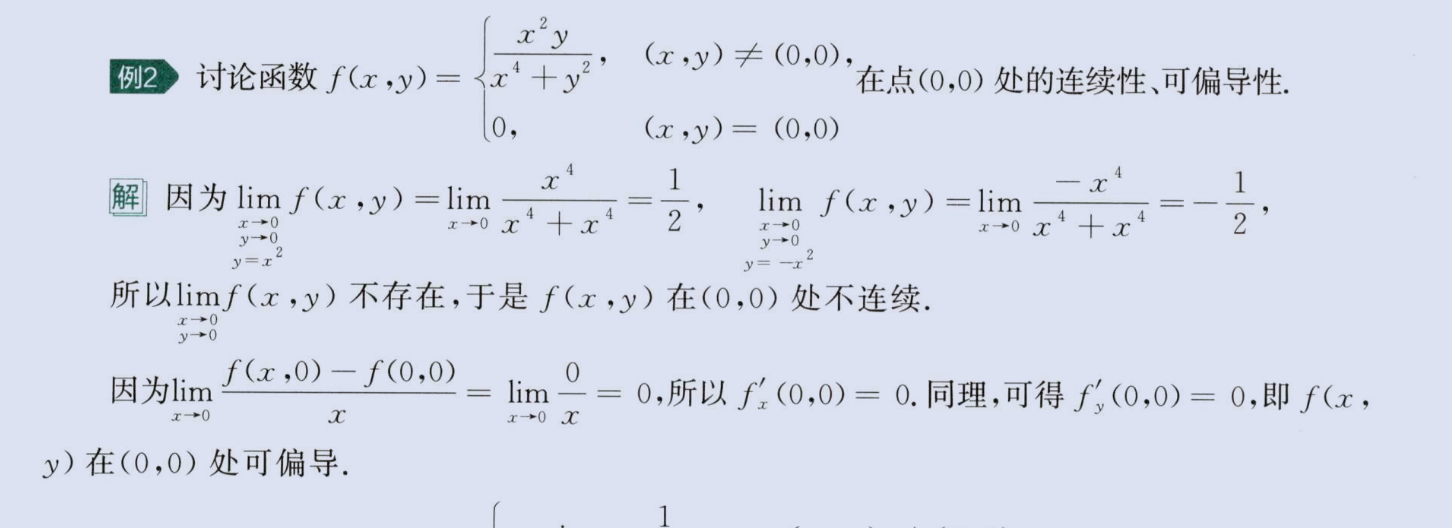 image-20230811204554671
image-20230811204554671
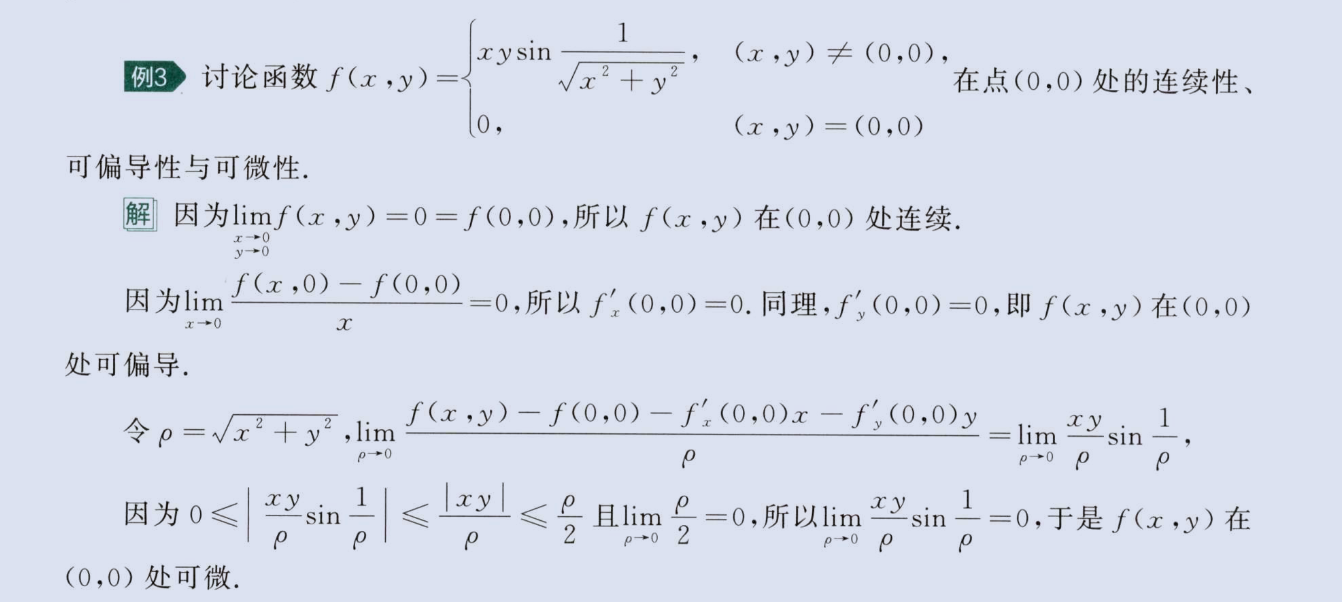 image-20230811204909079
image-20230811204909079
显函数求偏导
 image-20230811205144145
image-20230811205144145
复合函数求偏导
 image-20230811205459826
image-20230811205459826
 image-20230811205525953
image-20230811205525953
 image-20230811205704099
image-20230811205704099
隐函数(组)求导
 image-20230811205807051
image-20230811205807051
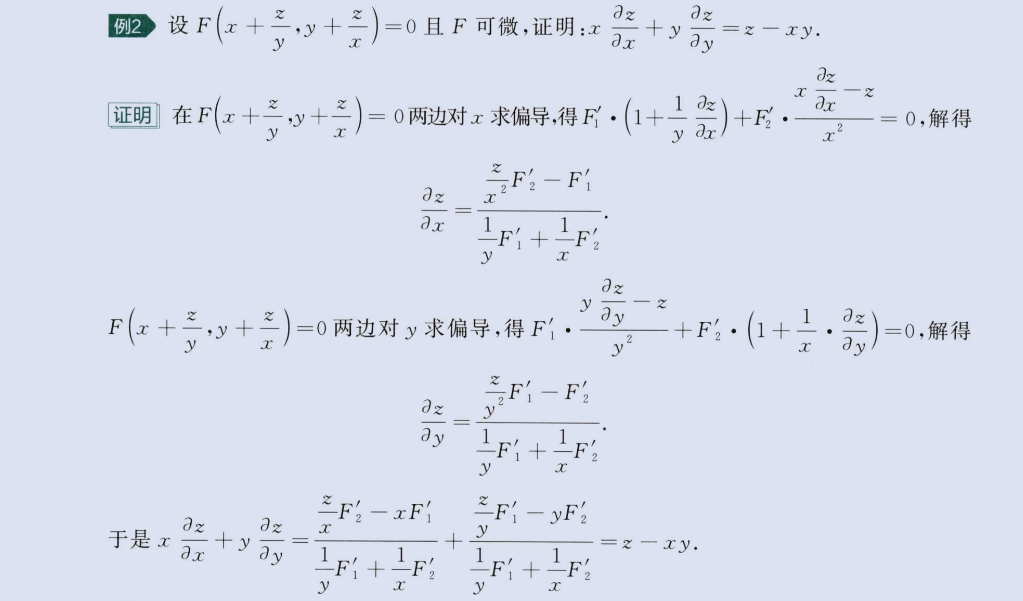 image-20230811205834996
image-20230811205834996
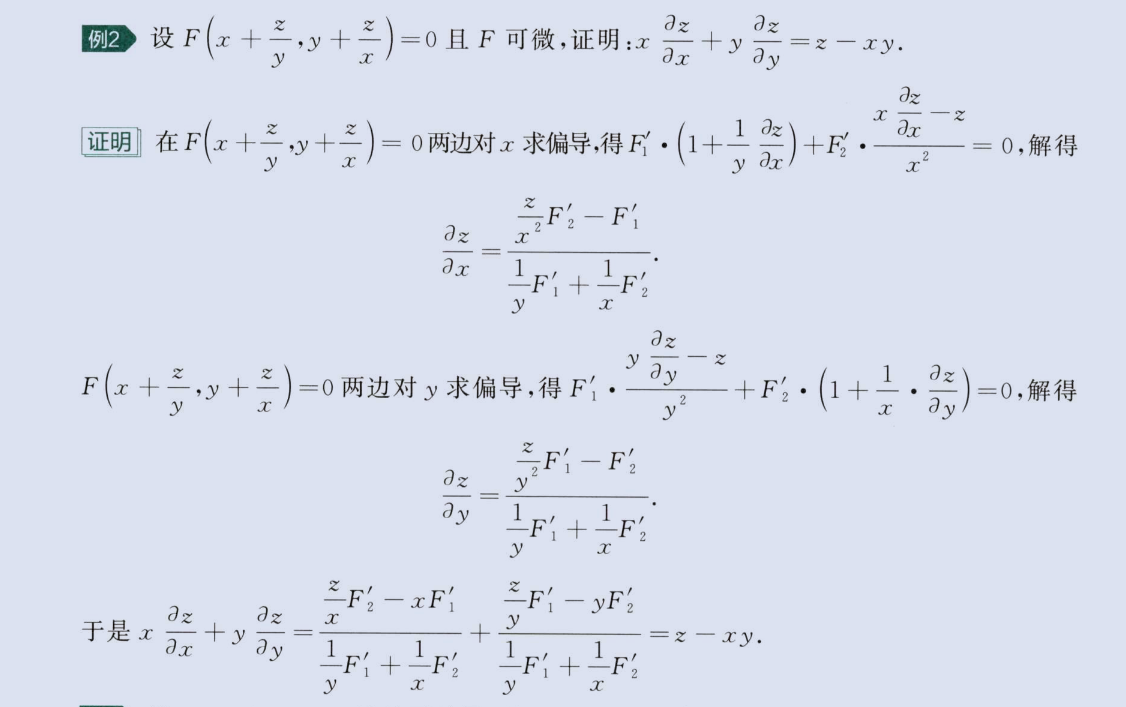 image-20230811210509287
image-20230811210509287
变换求偏导
 image-20230811210957748
image-20230811210957748
 image-20230811211011412
image-20230811211011412
求偏导反问题
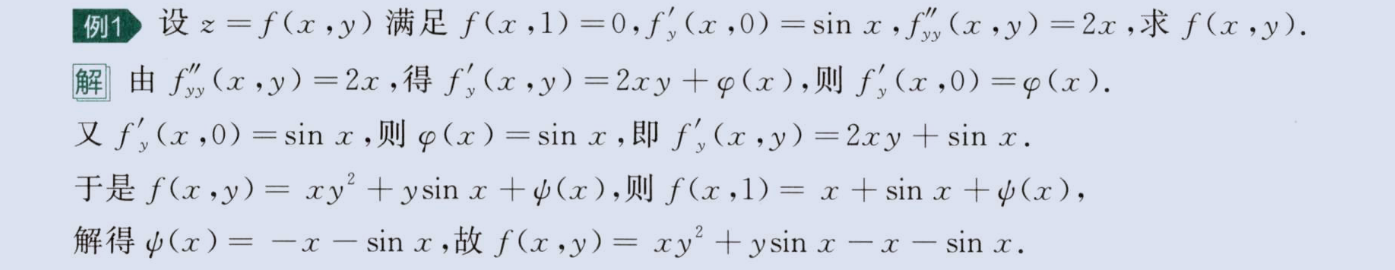 image-20230811211749235
image-20230811211749235
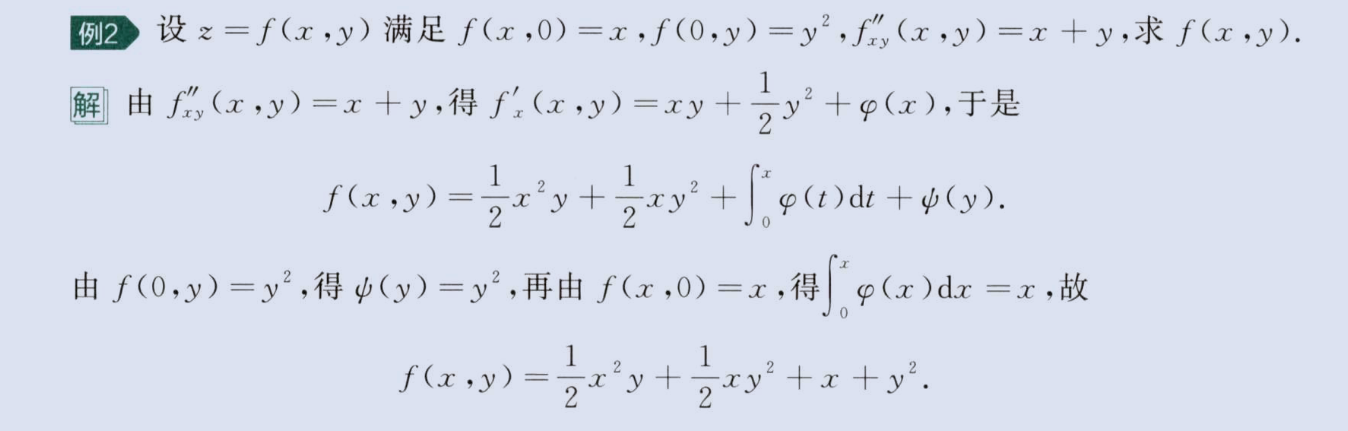 image-20230811211818102
image-20230811211818102
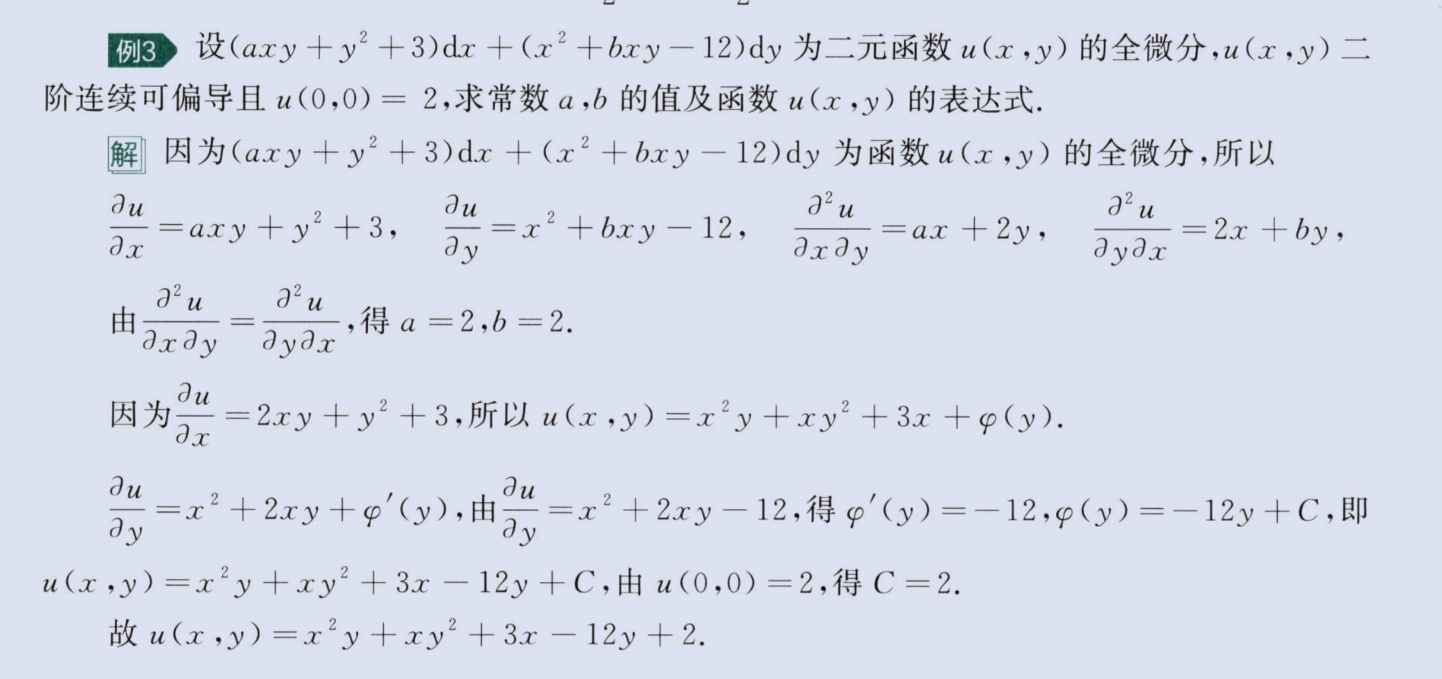 image-20230811211838515
image-20230811211838515
最值问题(拉格朗日数乘法)
 image-20230811212019115
image-20230811212019115
 image-20230811212150224
image-20230811212150224
 image-20230811212325296
image-20230811212325296
第七章-微分方程
高数
第七章 微分方程 (flowus.cn)
知识点
微分方程定义
 image-20230812223649582
image-20230812223649582
可分离变量的微分方程
 image-20230812224232793
image-20230812224232793
齐次微分方程
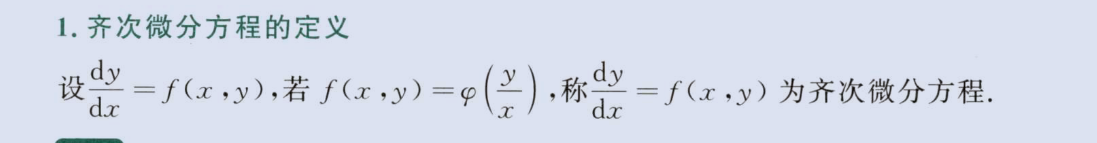 image-20230812224358944
image-20230812224358944
 image-20230812224507836
image-20230812224507836
 image-20230812224521550
image-20230812224521550
一阶齐次线性方程
 image-20230812224856037
image-20230812224856037
一阶齐次非线性方程
 image-20230812225009723
image-20230812225009723
可降阶的高阶微分方程
 image-20230812225804548
image-20230812225804548
 image-20230812225953014
image-20230812225953014
高阶线性微分方程概念
 image-20230812231600749
image-20230812231600749
高阶线性微分方程解的结构与性质
 image-20230812231126043
image-20230812231126043
二阶常系数齐次线性微分方程通解


 image-20230812230658351
image-20230812230658351
二阶常系数非齐次线性微分方程特解
 image-20230812230853624
image-20230812230853624
题型
概念
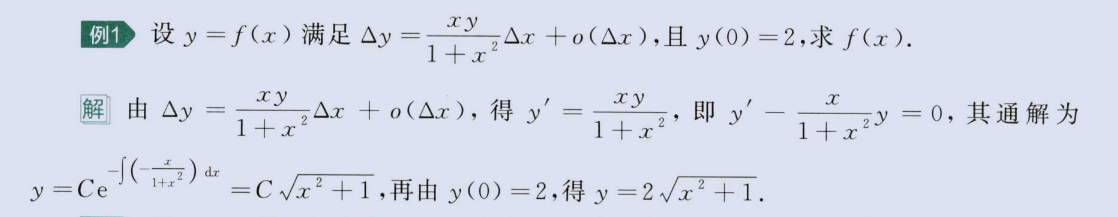 image-20230812231301115
image-20230812231301115
解的结构与性质
 image-20230812231431694
image-20230812231431694
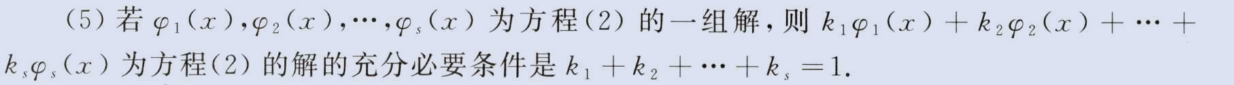 image-20230812231652438
image-20230812231652438
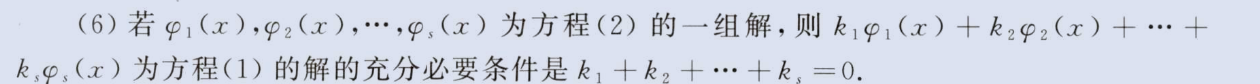 image-20230812231740137
image-20230812231740137
解一阶微分方程
1、齐次
 image-20230812231941694
image-20230812231941694
2、非齐次
 image-20230812232021063
image-20230812232021063
非特定类型微分方程
1、dy/dx 转 dx/dy
 image-20230812232144693
image-20230812232144693
2、整体代换
 image-20230812232459531
image-20230812232459531
可降阶的微分方程
1、缺 y
 image-20230812232724600
image-20230812232724600
2、缺 x
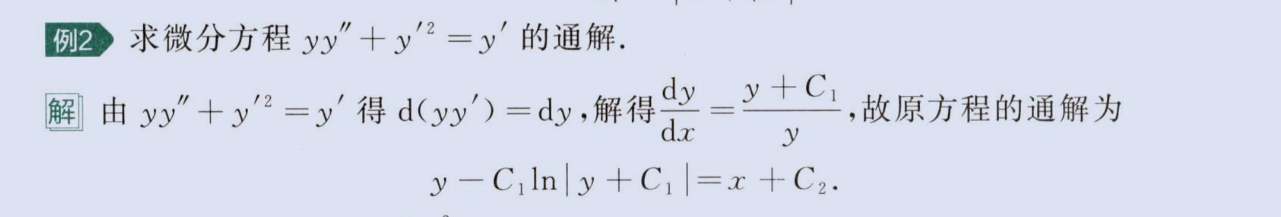 image-20230812232902101
image-20230812232902101
高阶常系数线性微分方程解的结构
 image-20230812234802960
image-20230812234802960
二阶非齐次
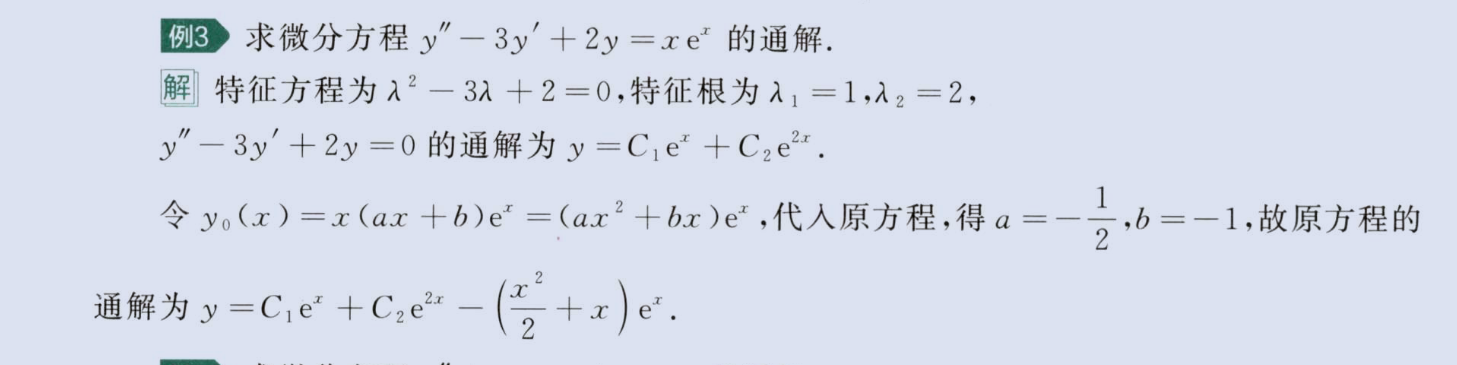 image-20230812234615786
image-20230812234615786
 image-20230812234630095
image-20230812234630095
涉及到 r
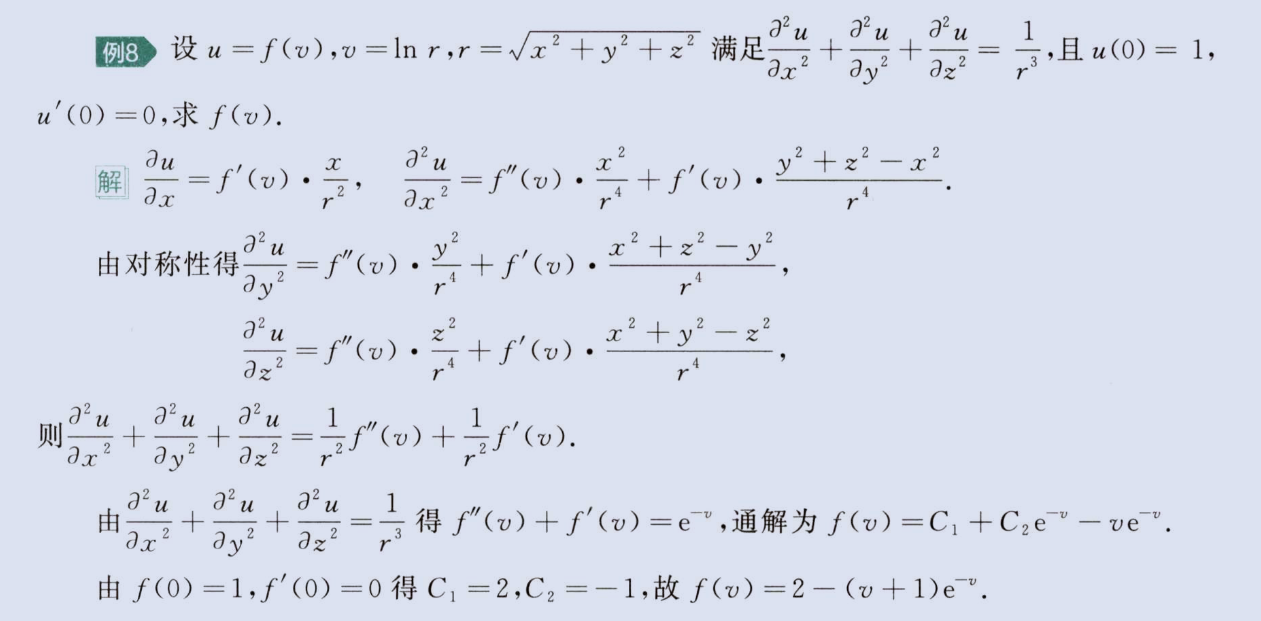 image-20230812234936488
image-20230812234936488
第八章-重积分
高数
第八章 重积分 (flowus.cn)
知识点
二重积分概念
 image-20230813151209133
image-20230813151209133
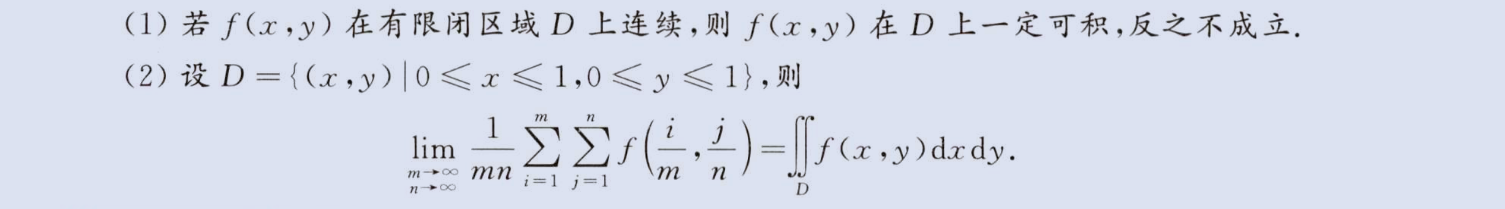 image-20230813151307692
image-20230813151307692
二重积分中值定理

二重积分对称性质
 image-20230813151539835
image-20230813151539835
二重积分计算
直角坐标法
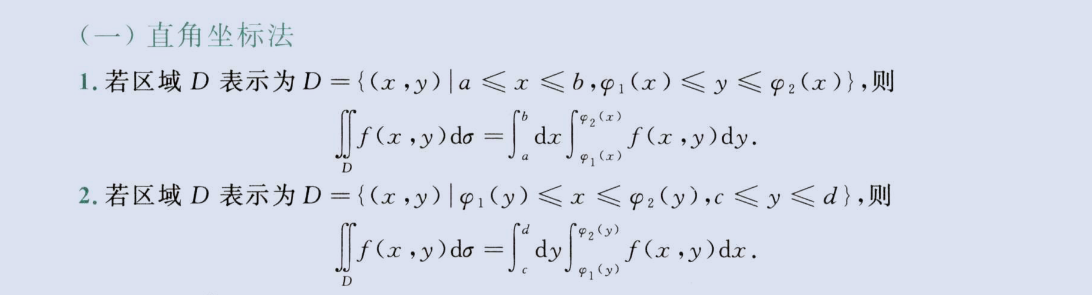 image-20230813151626765
image-20230813151626765
极坐标法
 image-20230813151709742
image-20230813151709742
二重积分几何应用
 image-20230813151831213
image-20230813151831213
题型
二重积分概念
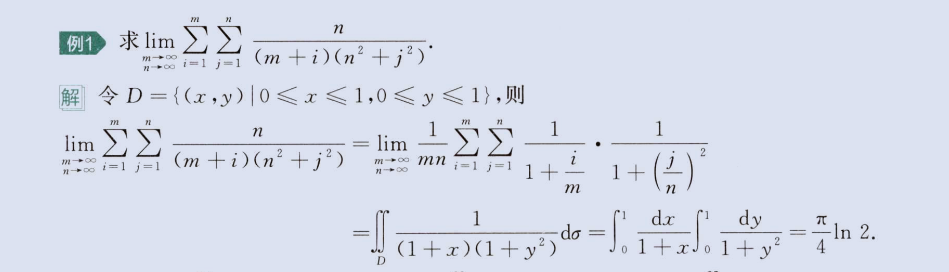 image-20230813151924583
image-20230813151924583
二重积分对称性
1、轮换对称
 image-20230813152017663
image-20230813152017663
2、奇偶性
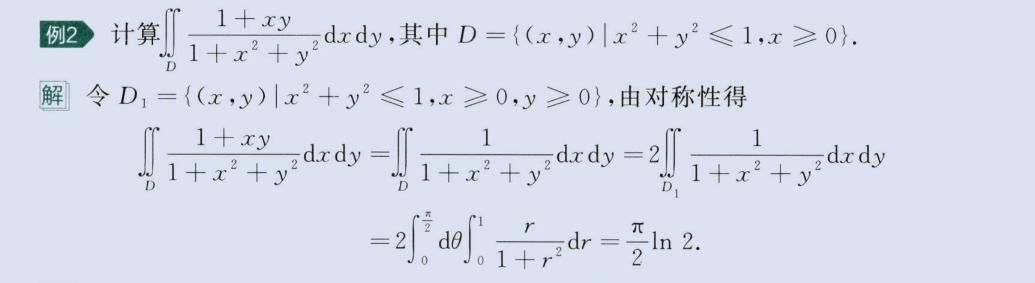 image-20230813153430435
image-20230813153430435
二重积分中值定理
 image-20230813152210362
image-20230813152210362
改变积分次序‘
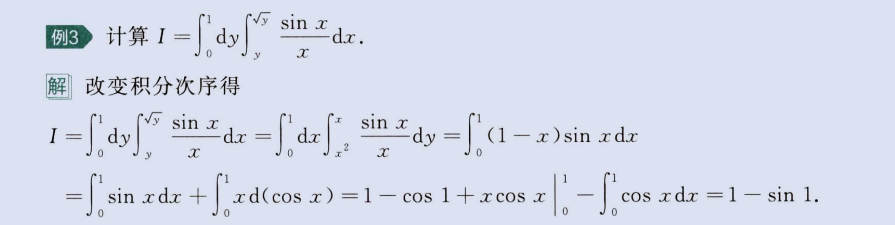 image-20230813152422502
image-20230813152422502
改变积分次序与变限积分求导
 image-20230813152611285
image-20230813152611285
二重积分与参数方程
 image-20230813152826853
image-20230813152826853
二重积分与极坐标
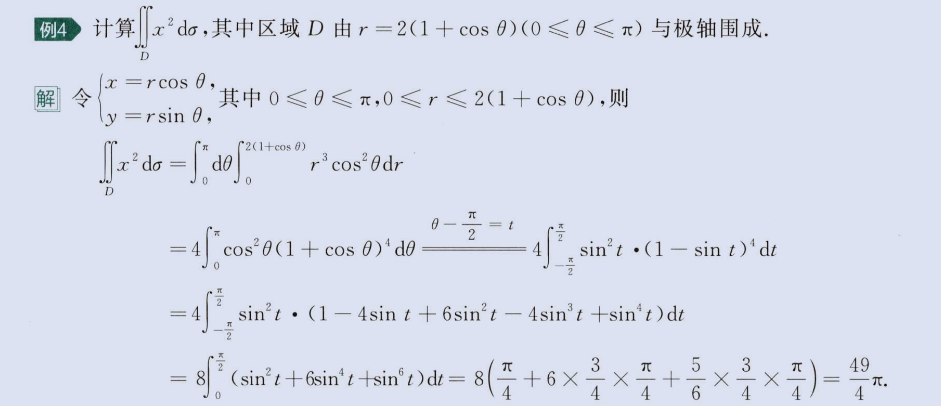 image-20230813152928208
image-20230813152928208
二重积分与偏导
 image-20230813153106507
image-20230813153106507


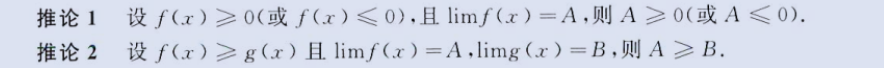






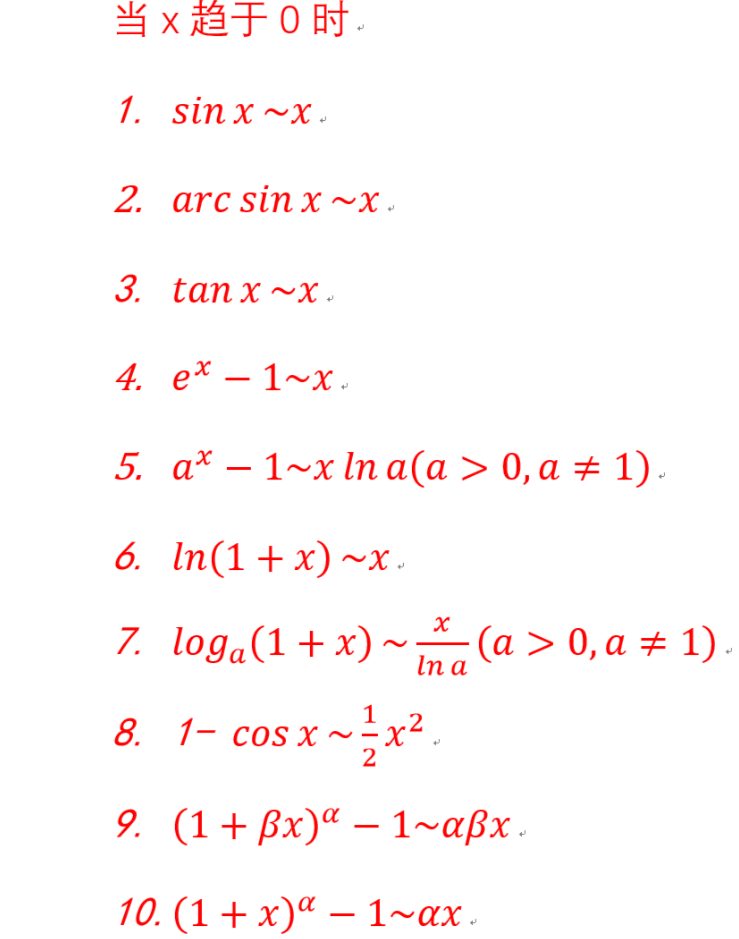




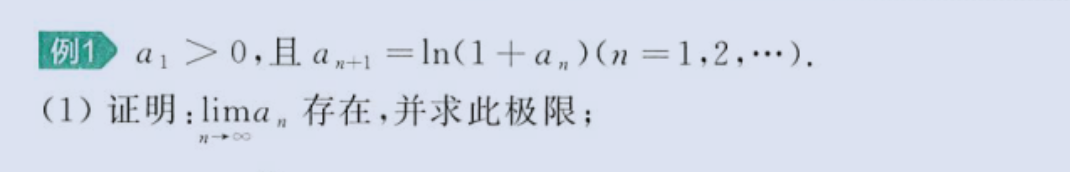



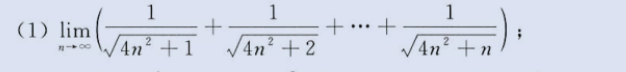
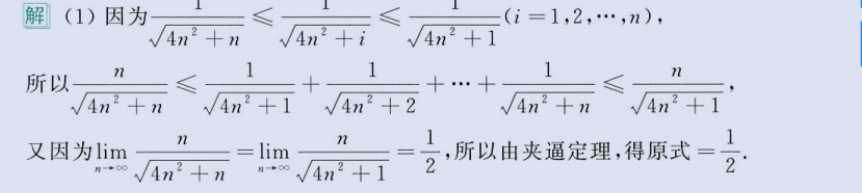
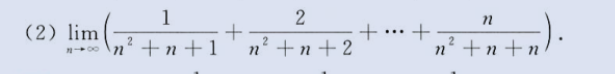
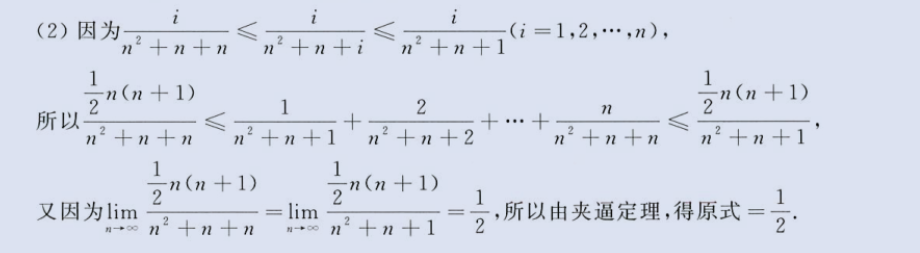
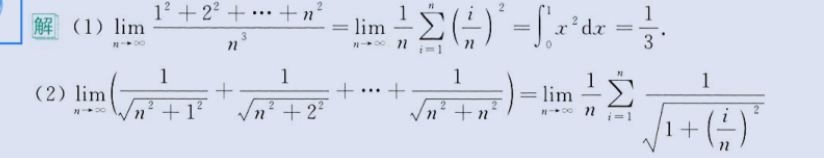
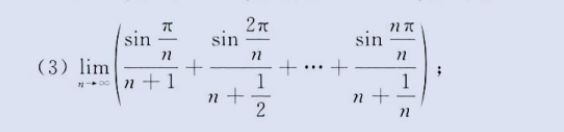
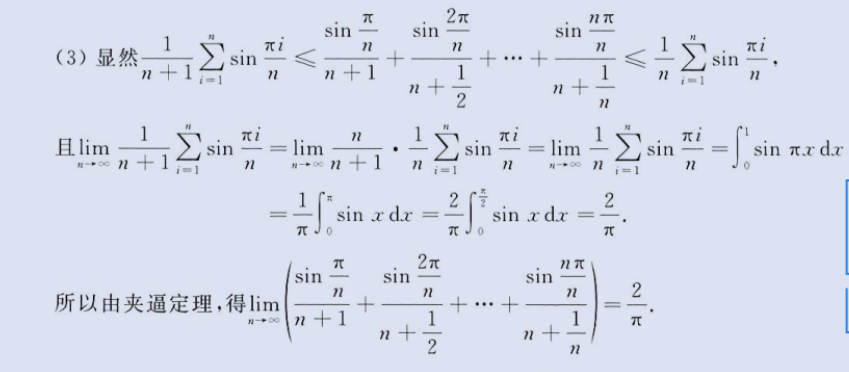
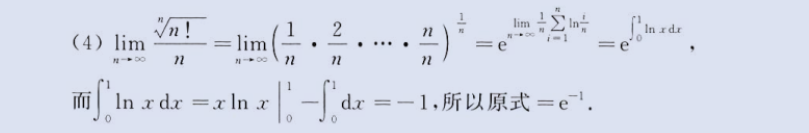

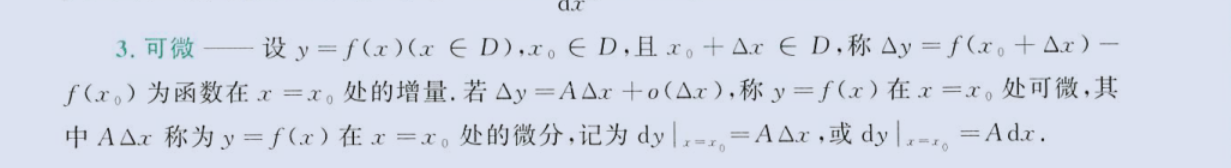

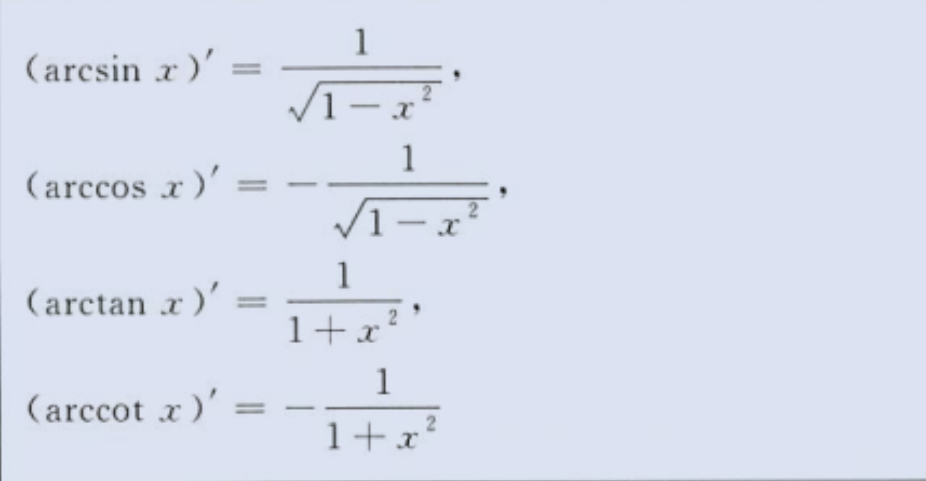


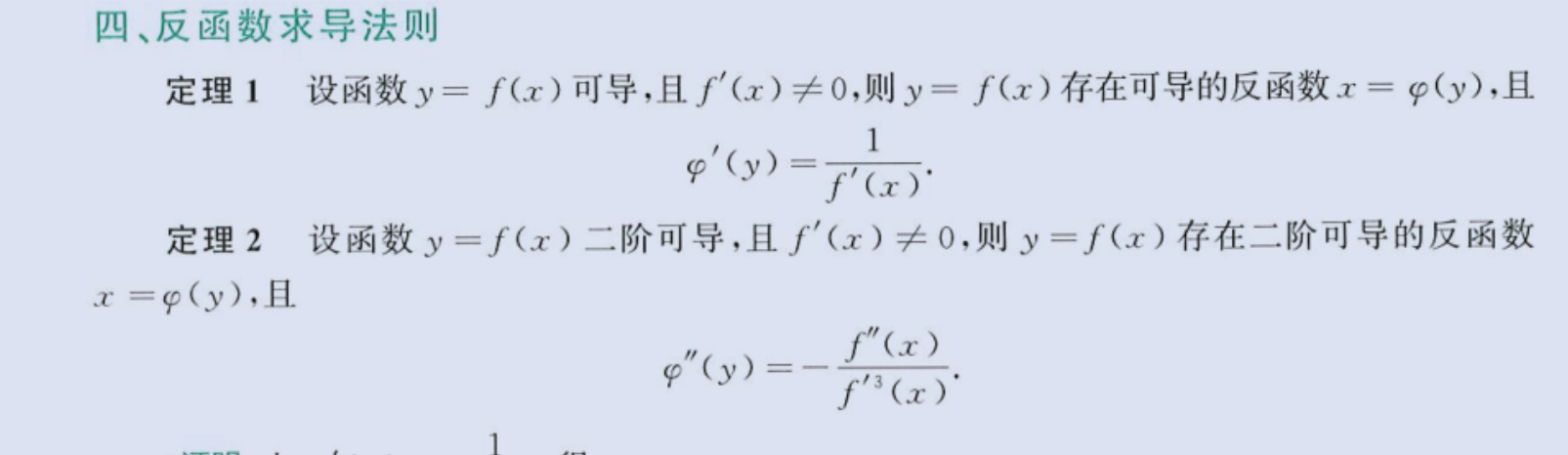


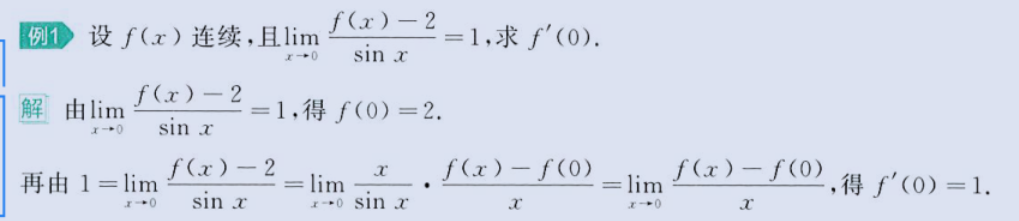


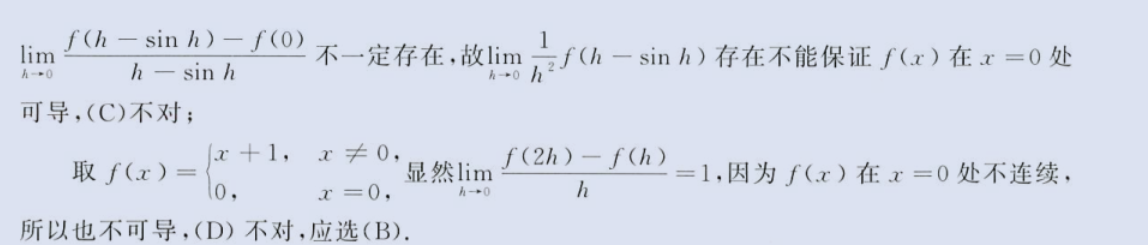
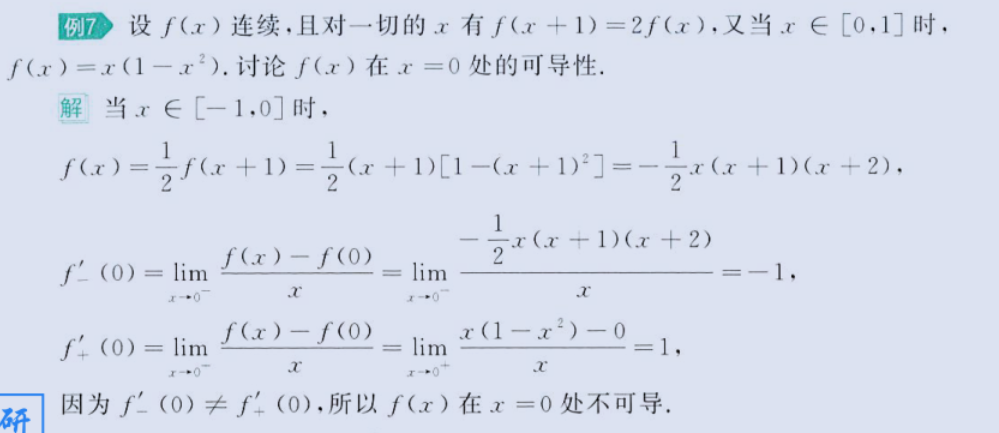







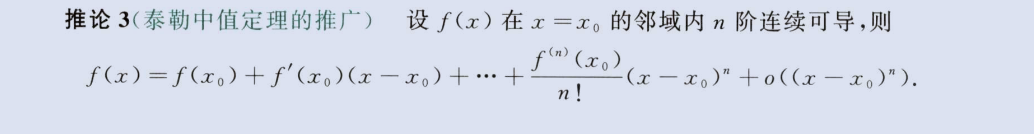





























 3、结论中含两个中值 ξ 和
η,且对应项完全相等
3、结论中含两个中值 ξ 和
η,且对应项完全相等