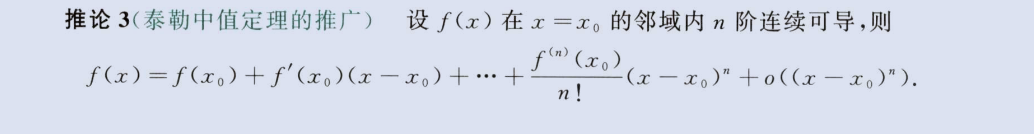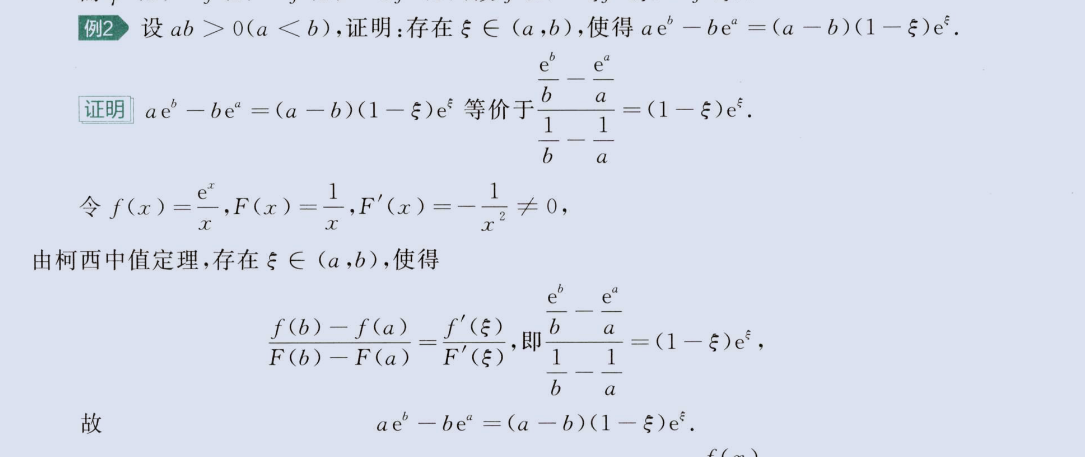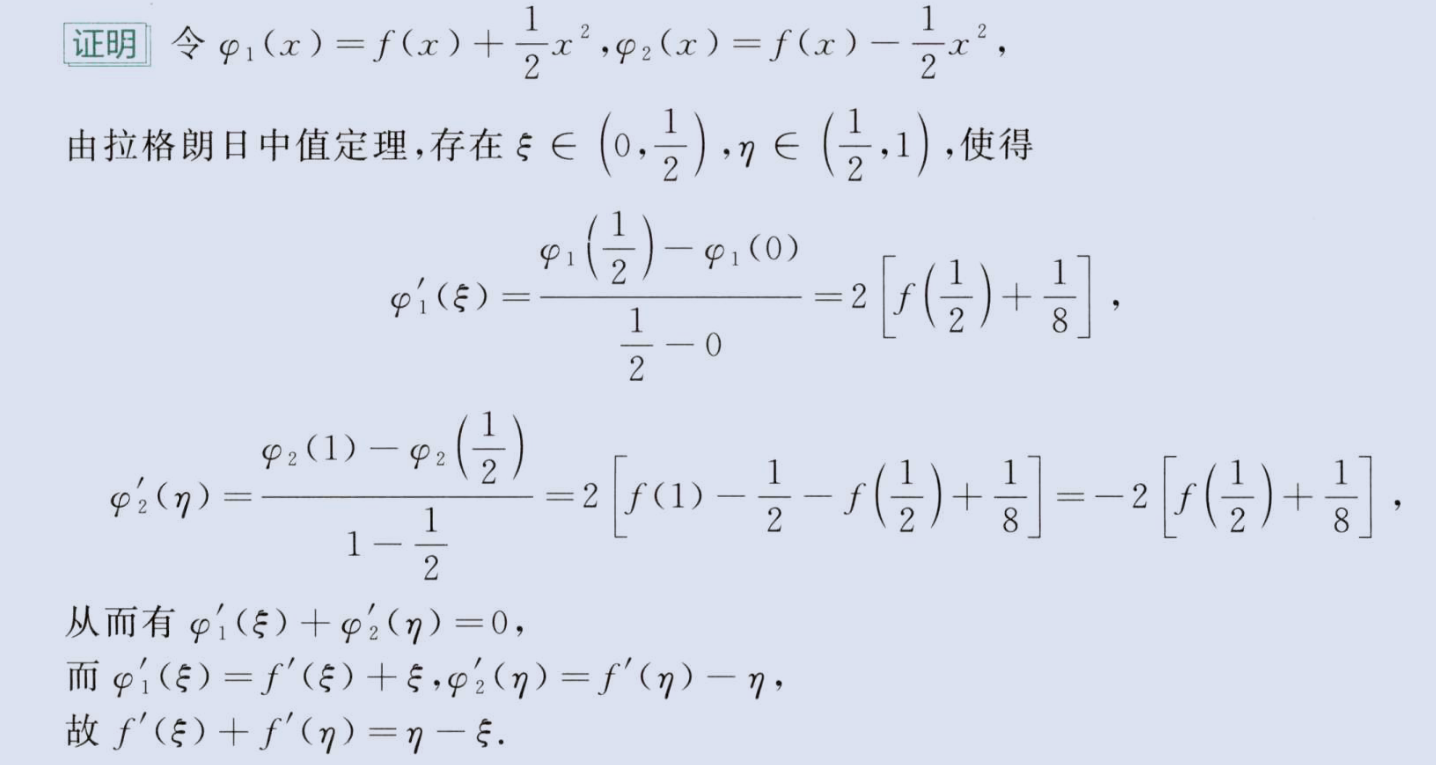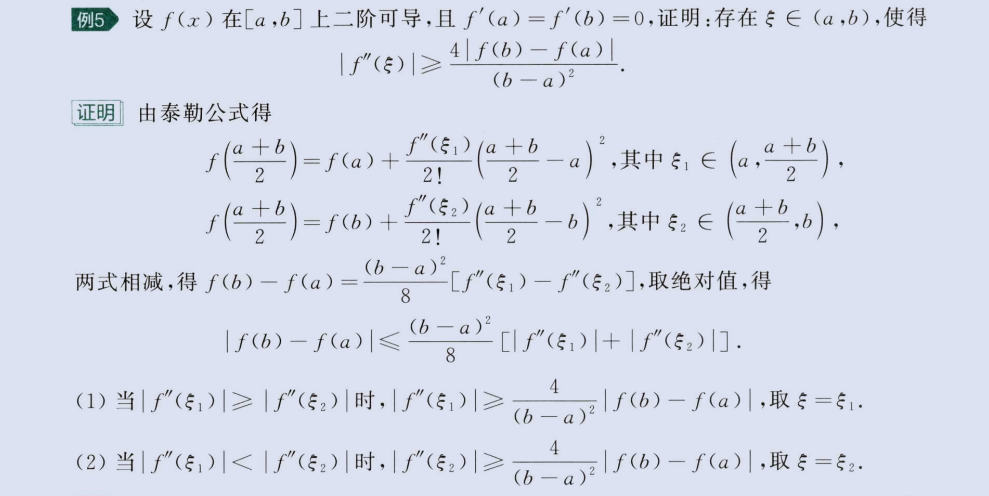高数
第三章 一元函数微分学的应用 (flowus.cn)
第三章-一元函数微分学的应用
知识点
罗尔中值定理
image-20230804093843135
拉格朗日中值定理
image-20230804093906737
柯西中值定理
image-20230804094214170
泰勒中值定理
image-20230804094309860
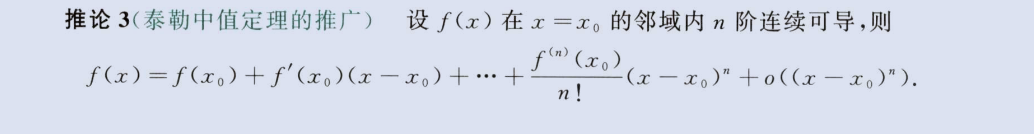image-20230804095002711
麦克劳林公式
导数零点定理
image-20230804094715790
导数介值定理
image-20230804094932182
弧微分
image-20230804095307798
曲率半径
image-20230804095355735
积分中值定理
image-20230804175948502
image-20230804175920152
题型
证明 n 阶导为0
1、导数介值定理
image-20230804100724787
2、罗尔定理
image-20230804100836589
3、拉格朗日中值定理
image-20230804101259571
证明结论为一个含中值 ξ
的方程 - 辅助函数
1、还原法 （ln型）
image-20230804101736670
image-20230804101915902
image-20230804102244964
image-20230804103713292
2、分组构造 （e型）
image-20230804103004508
看不出来可以考虑待定系数 e^kx [af(x)+bf'(x)]
image-20230804103853668
image-20230804104507575
3、凑微（移项）
image-20230804104851572
证明结论含 中值 ξ、a、b
1、a、b 与 ξ 可分离
image-20230804105253013
a、b、ξ 写成一个原函数
image-20230804105330189
a 、b 与 ξ 分离构造柯西
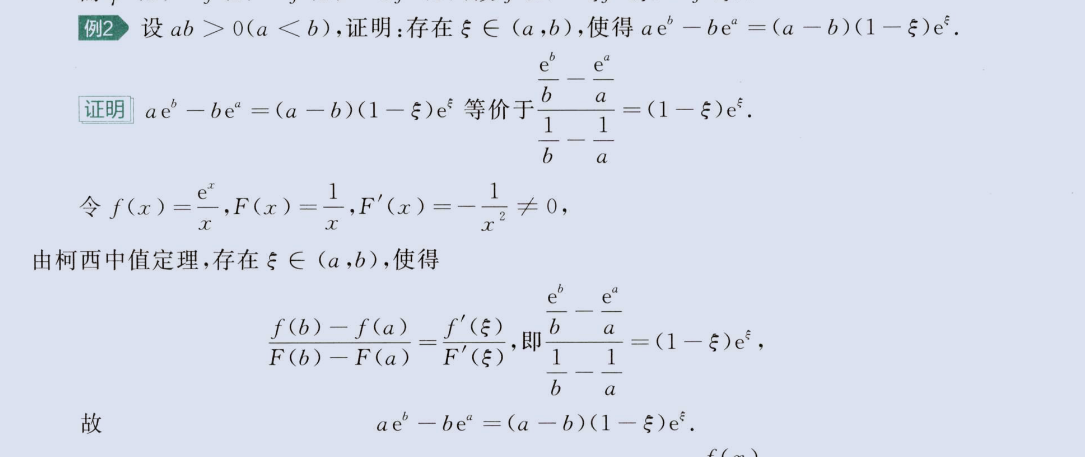image-20230804110110276
2、a 、b 与 ξ 不可分离
（凑微移项 ，ξ 换成 x）
image-20230804110243311
image-20230804110517025
image-20230804110638903
结论中含两个或以上中值
1、只含中值的导数
image-20230804110736392
image-20230804110903232
image-20230804111134645
2、两个中值项复杂度不同
image-20230804111538535
两次拉格朗日
image-20230804111550943
柯西+拉格朗日（柯西移项配凑拉格朗日）
image-20230804111753235
image-20230804111937780
3、结论中含两个中值 ξ
和 η，且对应项完全相等
image-20230804172414293
image-20230804172442124
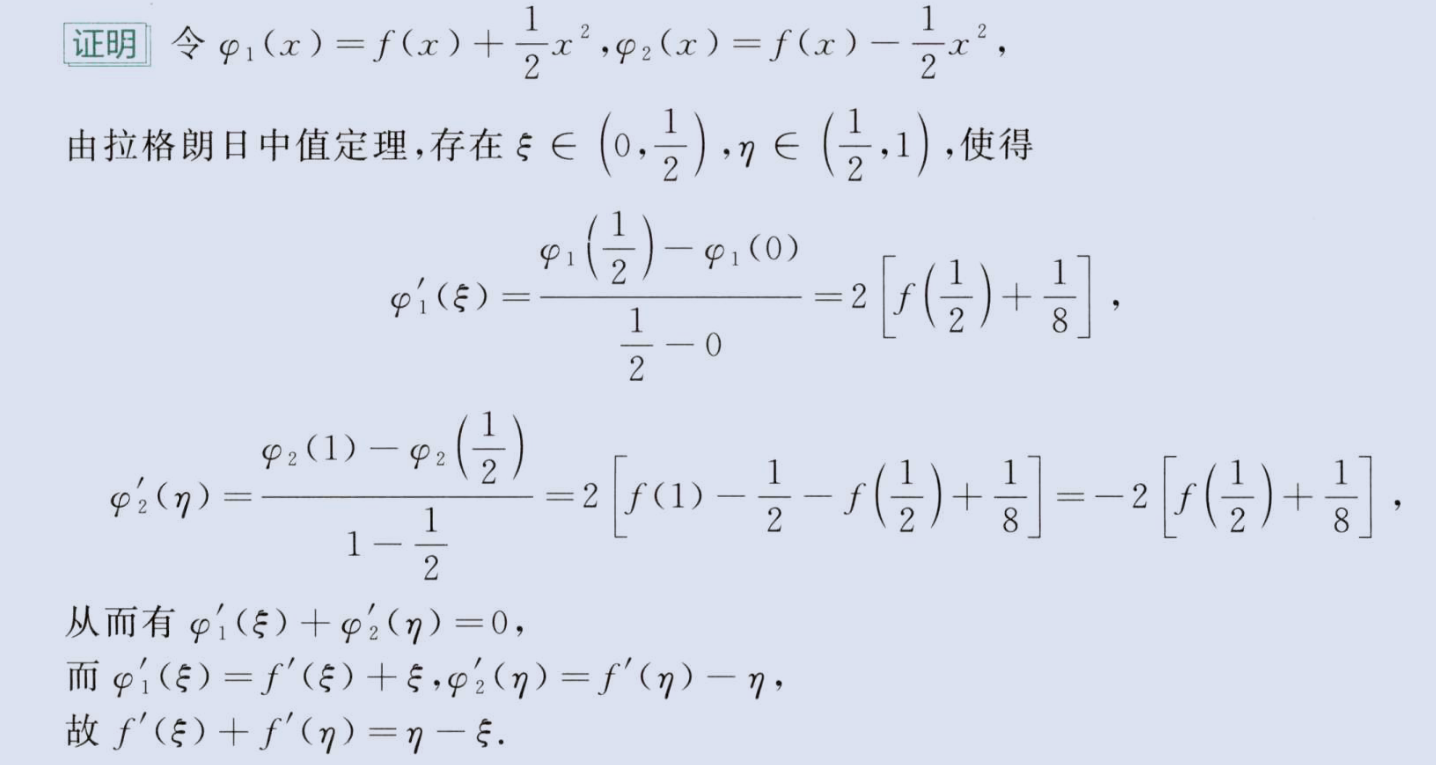image-20230804172505249
中值定理中的 θ
1、泰勒中值定理
image-20230804173054665
2、推广的积分中值定理
image-20230804175602141
拉格朗日常规
image-20230804181646070
image-20230804181636957
泰勒中值定理常规
1、相同点展开
image-20230804181025816
2、不同点展开
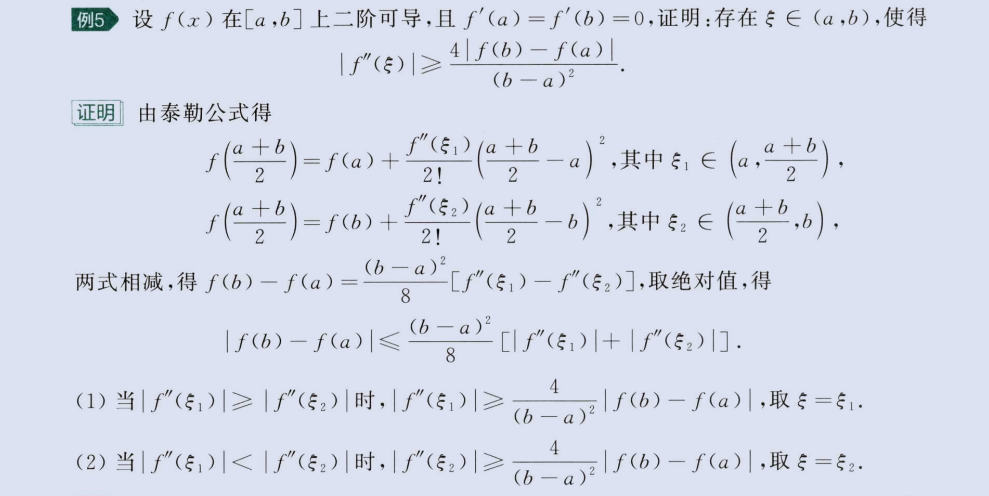image-20230804181401262
二阶导保号性 +
中值定理（实际上是导数单调性问题）
image-20230804182512202
1、 与拉格朗日
image-20230804182654479
2、与泰勒中值定理
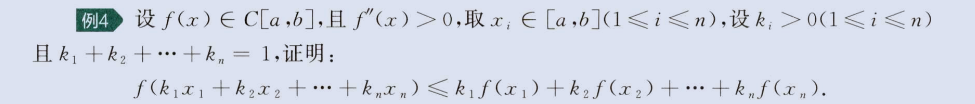image-20230804182755308
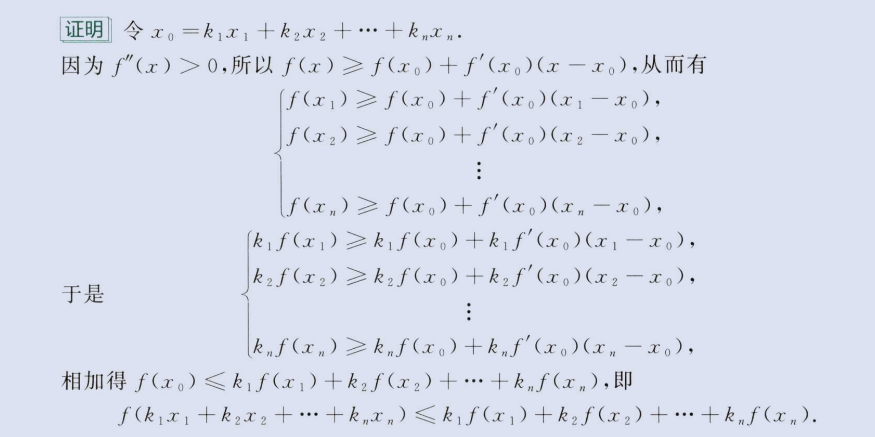image-20230804182419183
不等式证明与中值定理、凹凸性
1、与拉格朗日
image-20230804183121631
2、与柯西中值定理
image-20230804183313477
3、与凹凸性
image-20230804183436383
函数零点与方程的根
image-20230804215030303
原函数与罗尔定理
image-20230804215153533
拉格朗日中值定理与放缩
image-20230804215852617
vv
