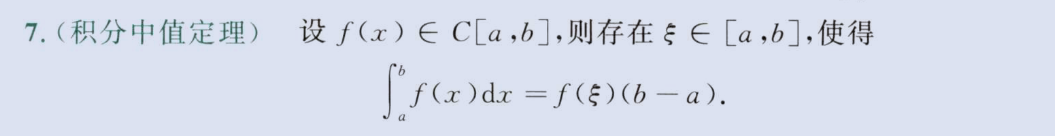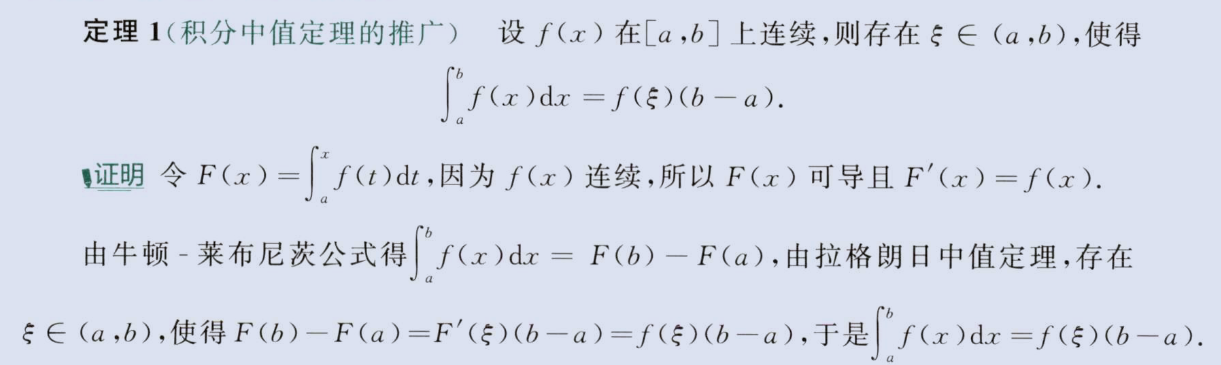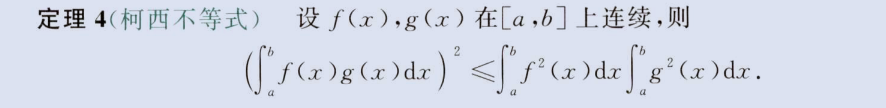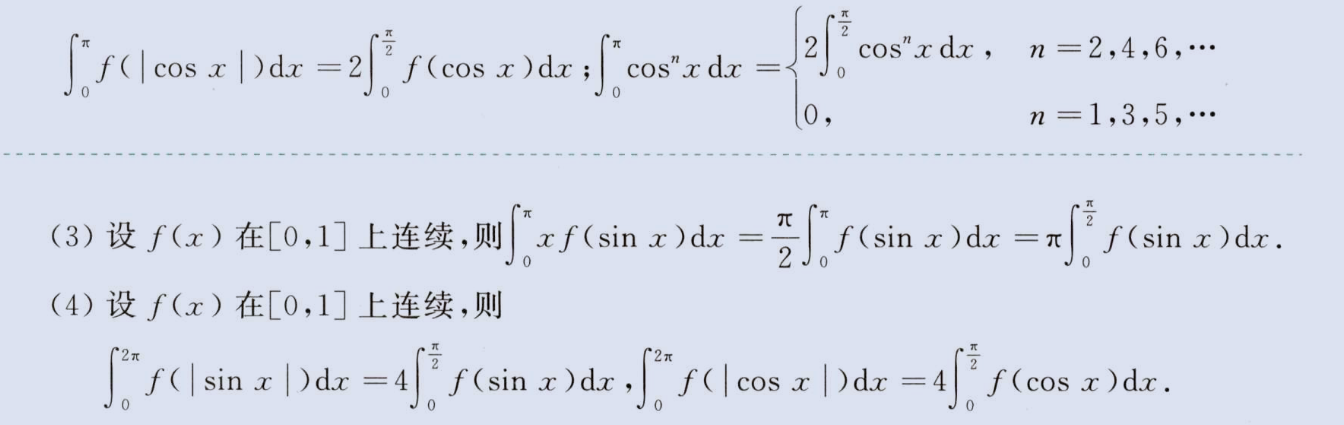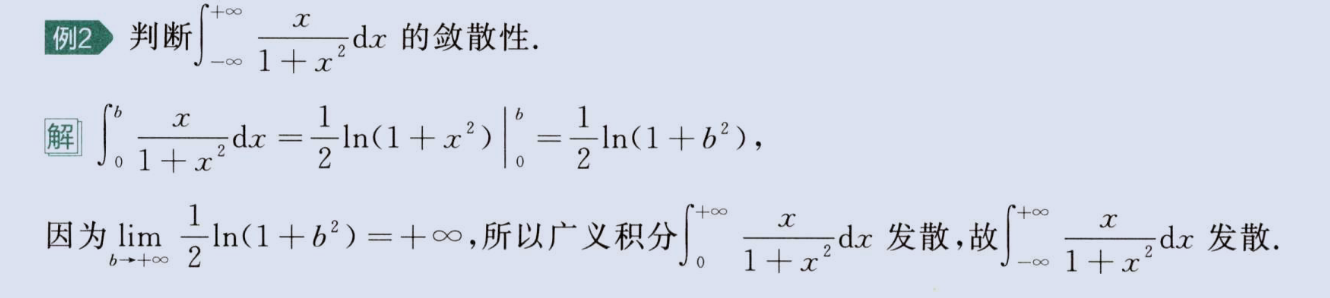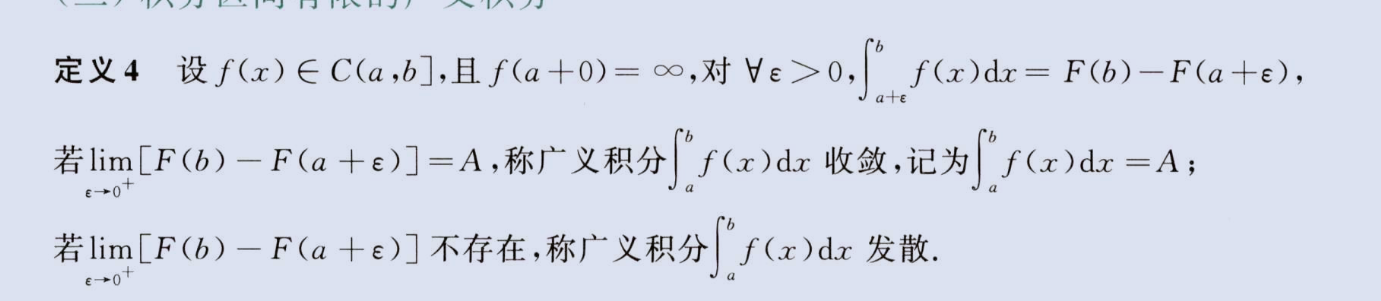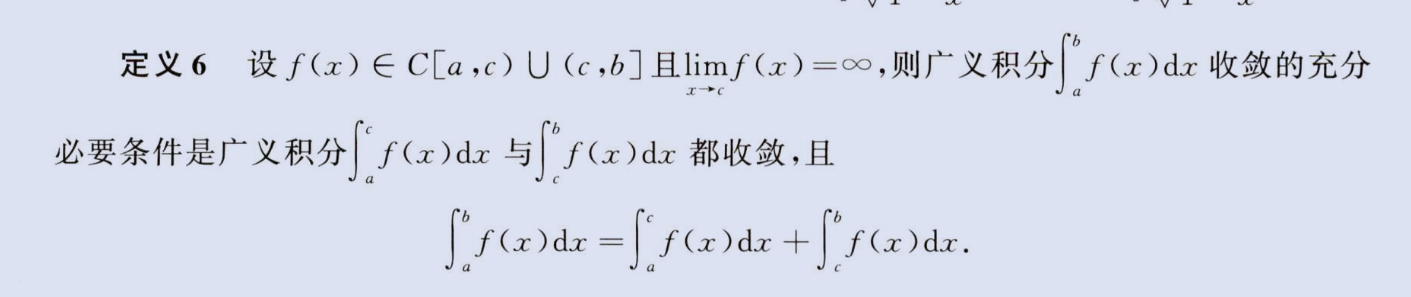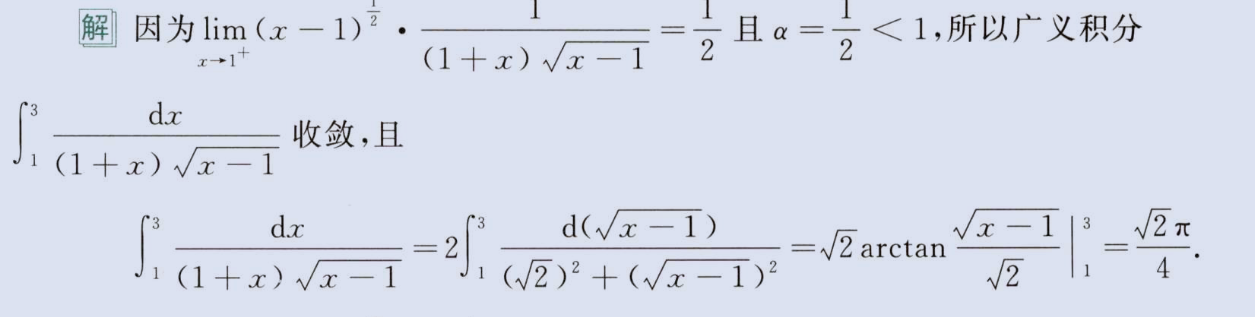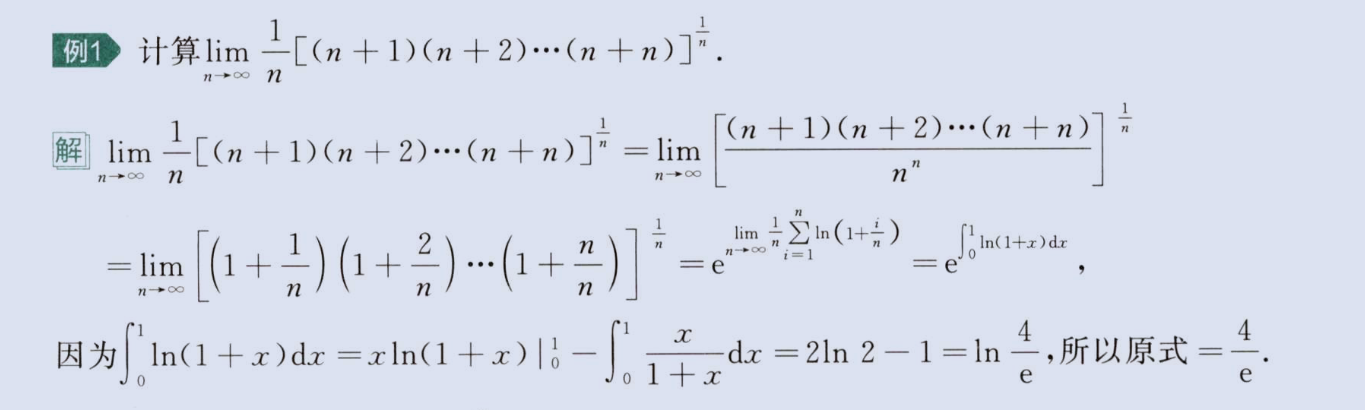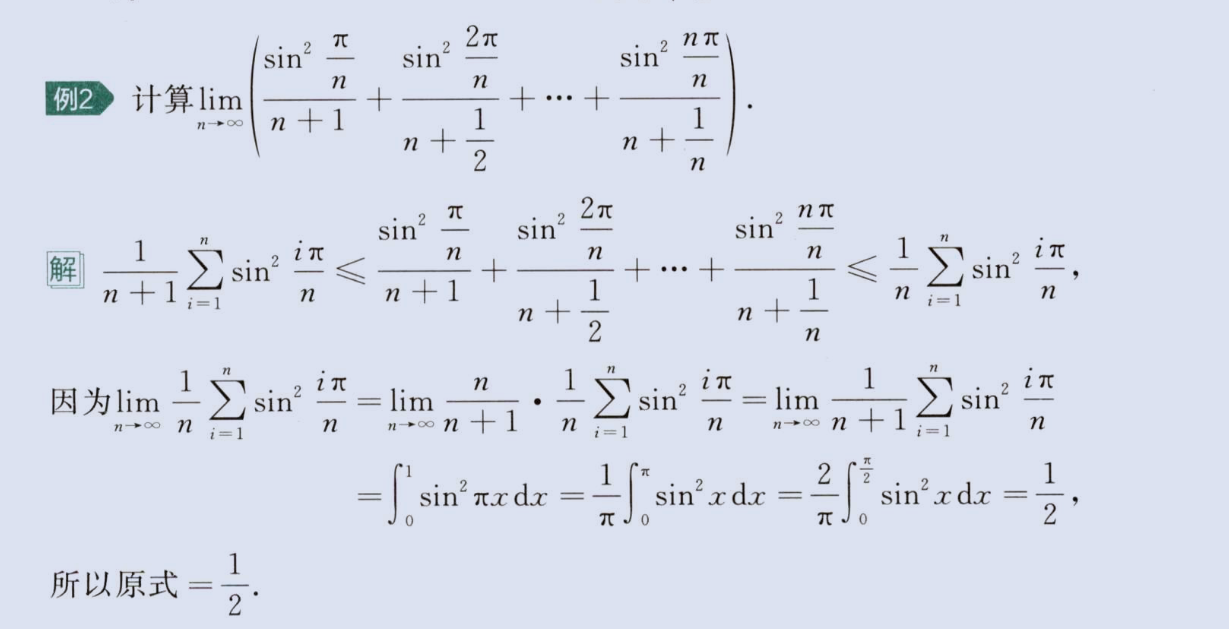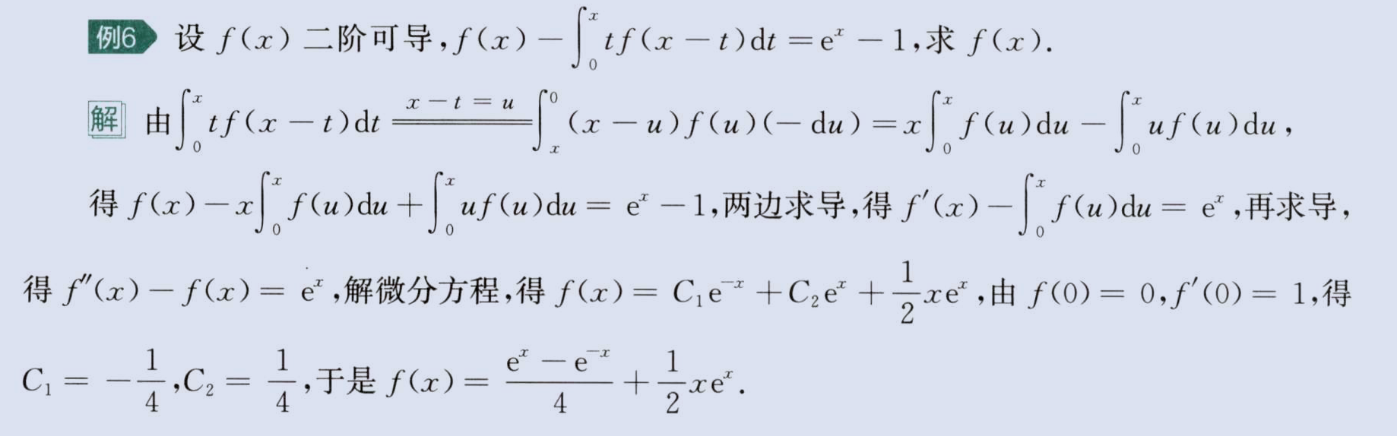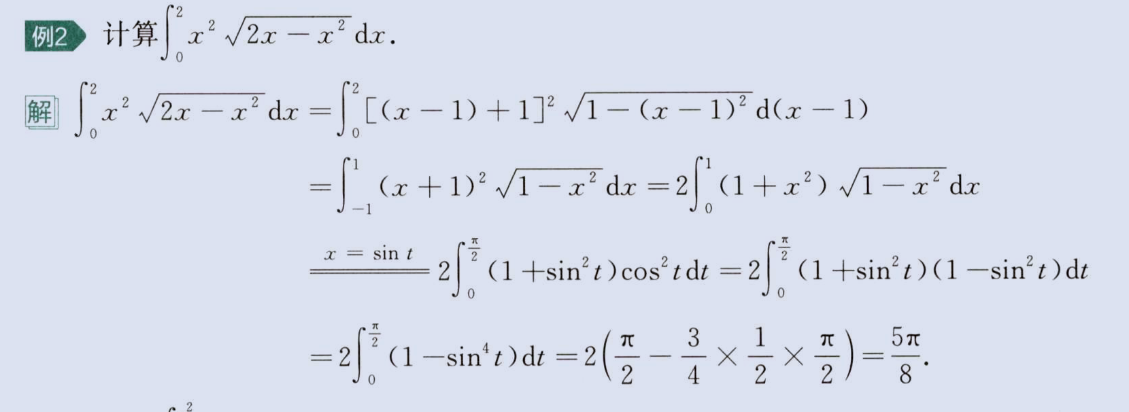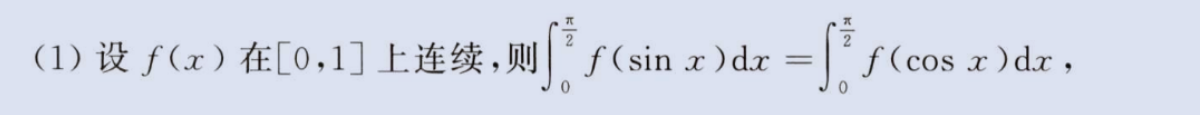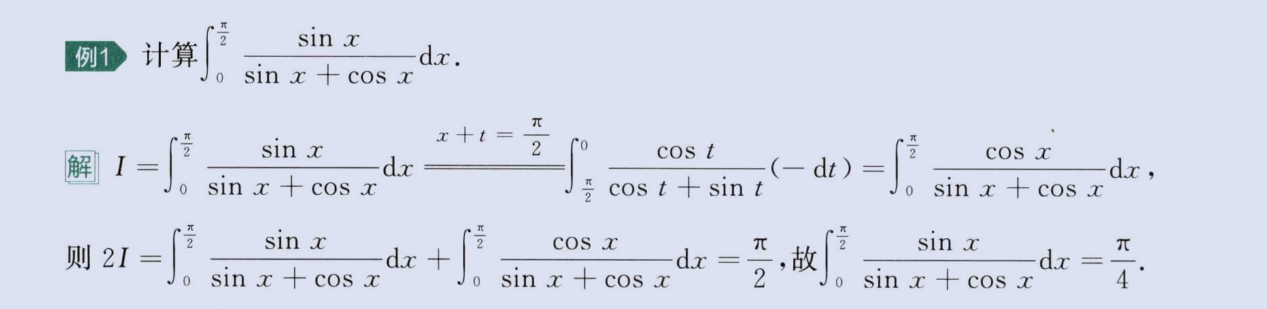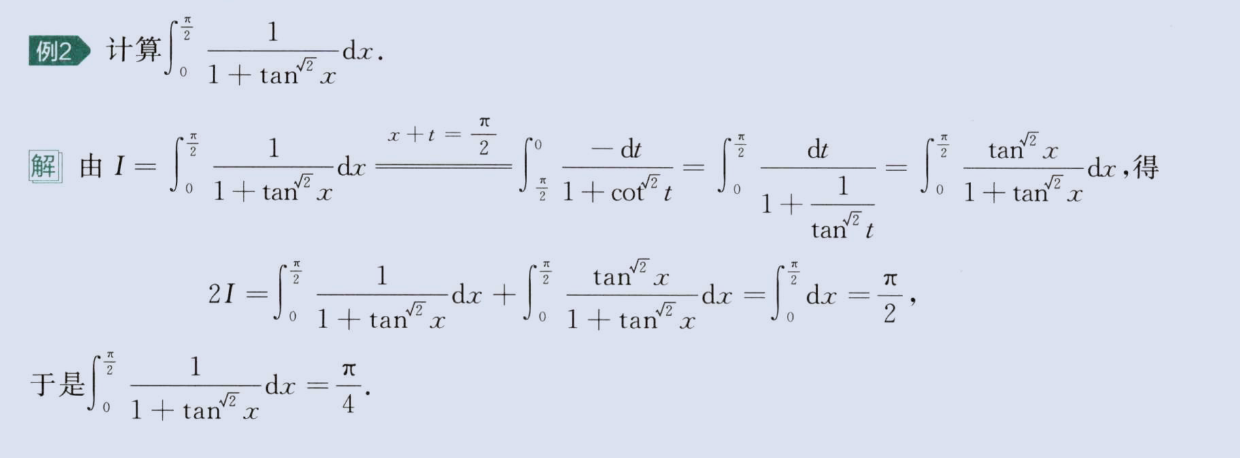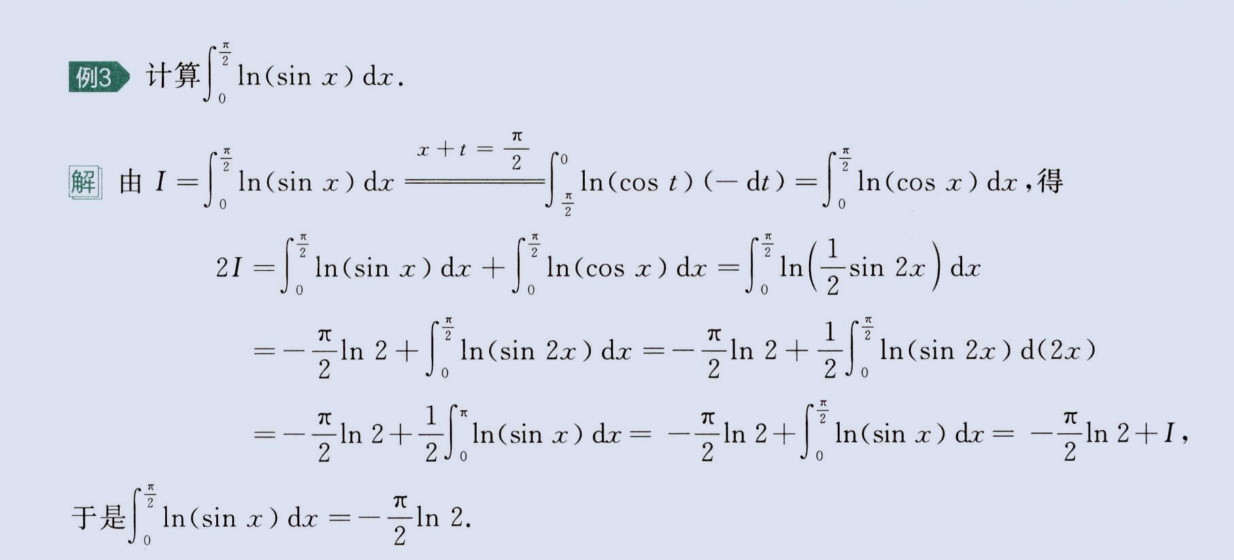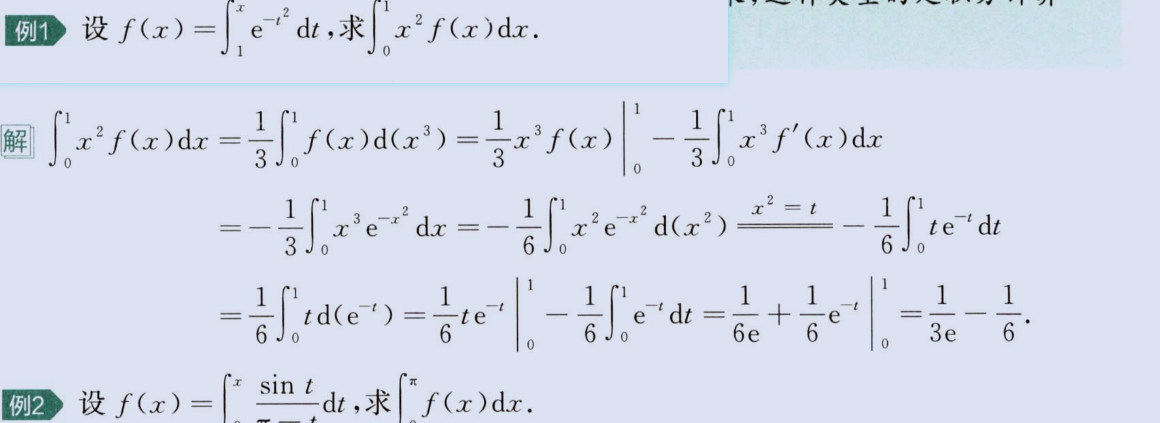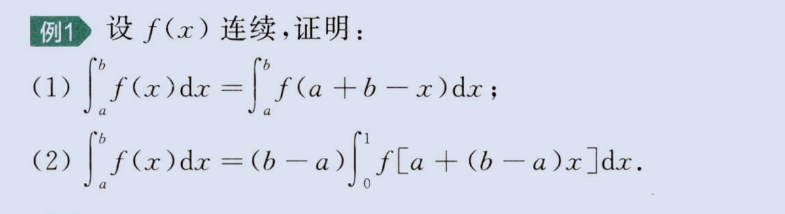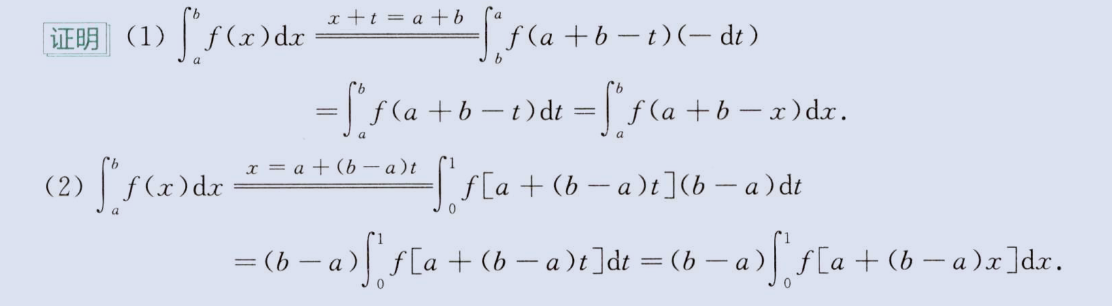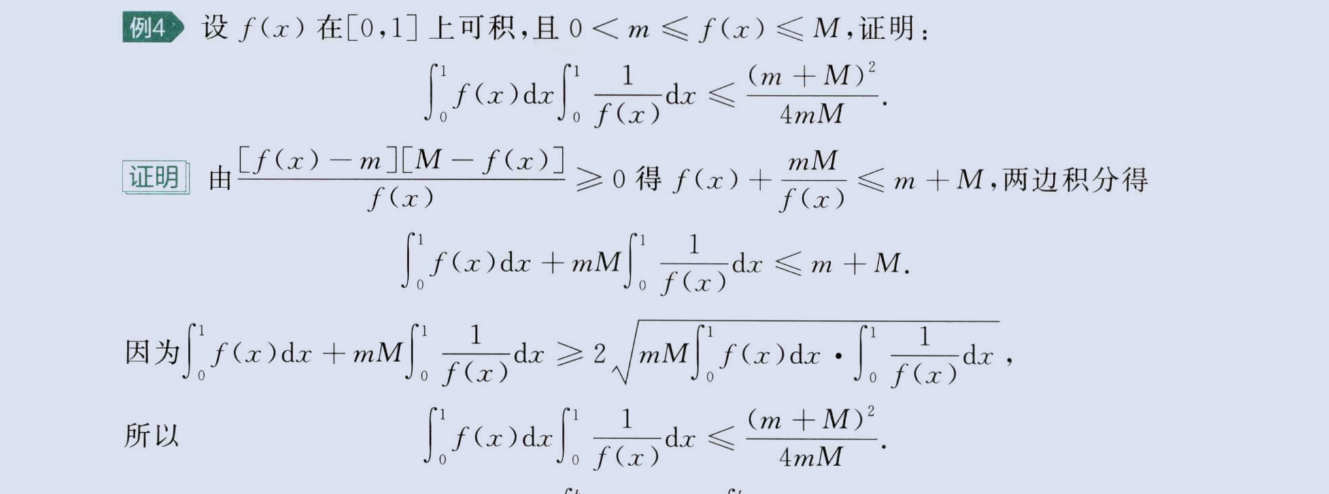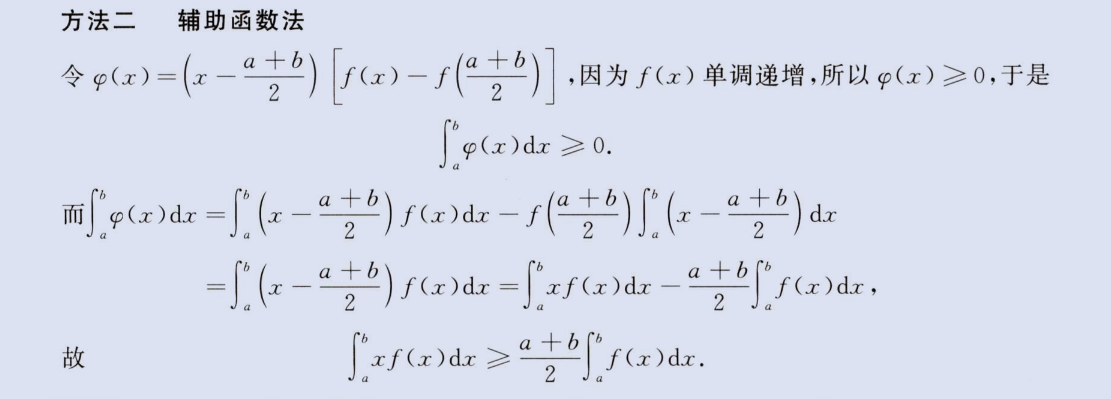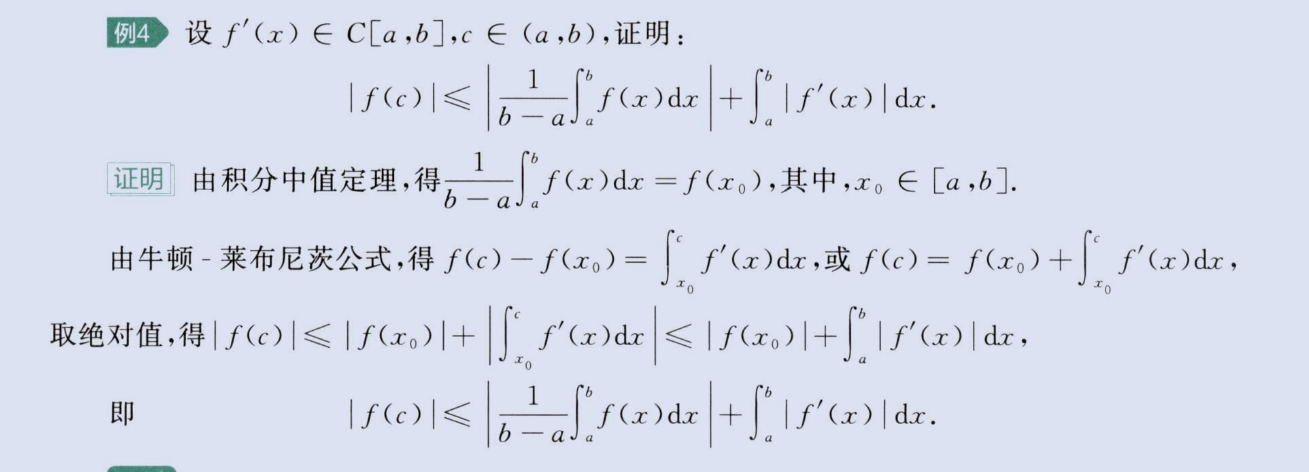高数
第五章 定积分 (flowus.cn)
知识点
定积分定义
image-20230806135657839
积分中值定理
介值定理推导，闭区间
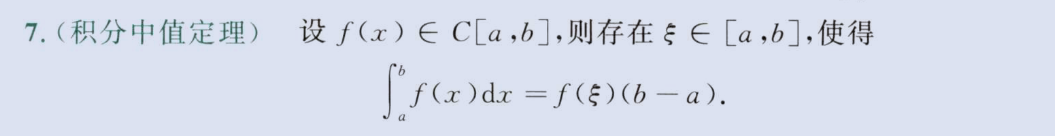image-20230806141052742
推广的积分中值定理
拉格朗日推导，开区间
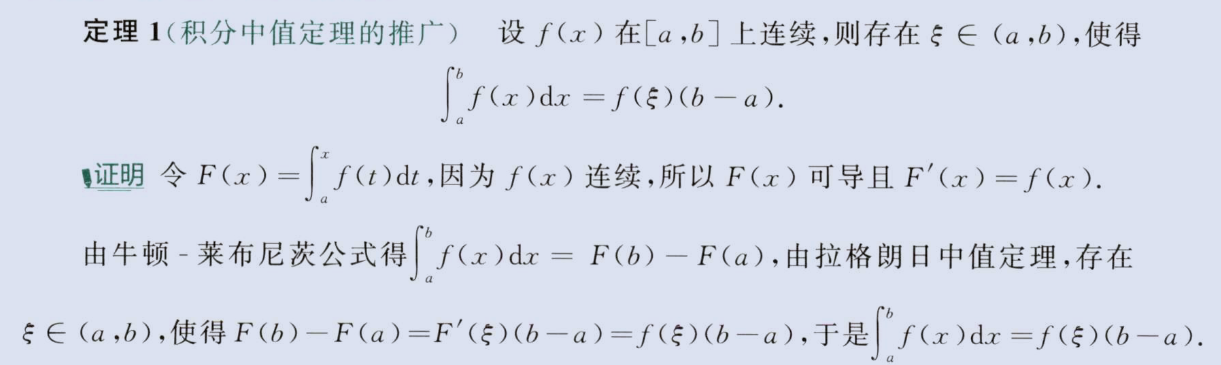image-20230806141244834
积分第一中值定理
介值定理推导，闭区间
积分柯西不等式
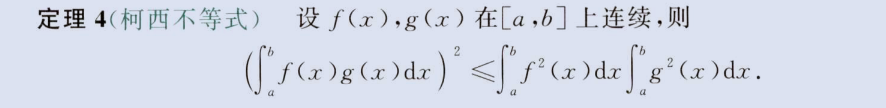image-20230806141547750
三角函数定积分
注意第（3）点，换元 （Π-x）=u 证明
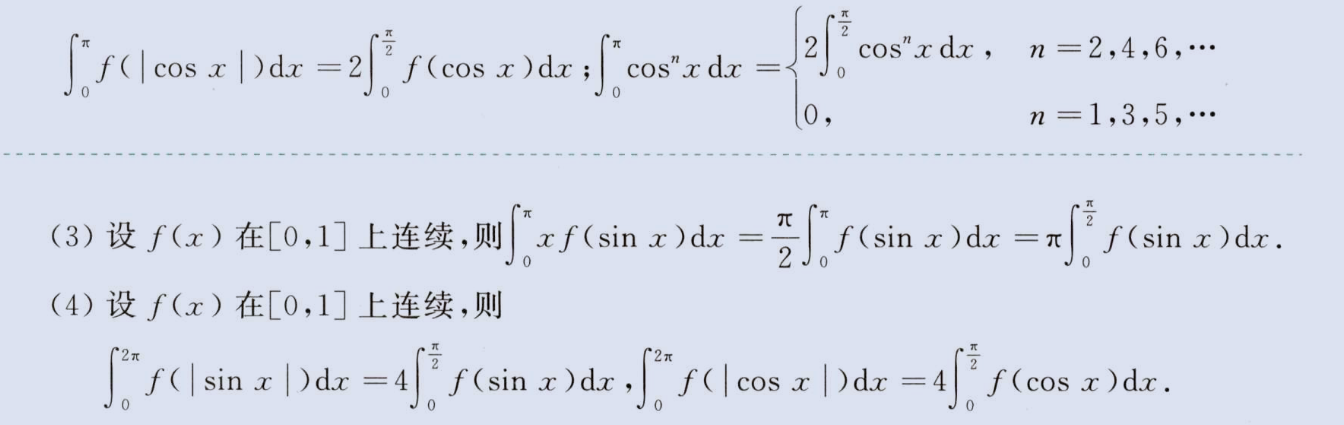image-20230806142401472
广义积分敛散性（积分区间无限）
image-20230806151452465
image-20230806151505030
image-20230806151532587
注意定义3，区间左右无穷，左右都要收敛才能收敛，如下
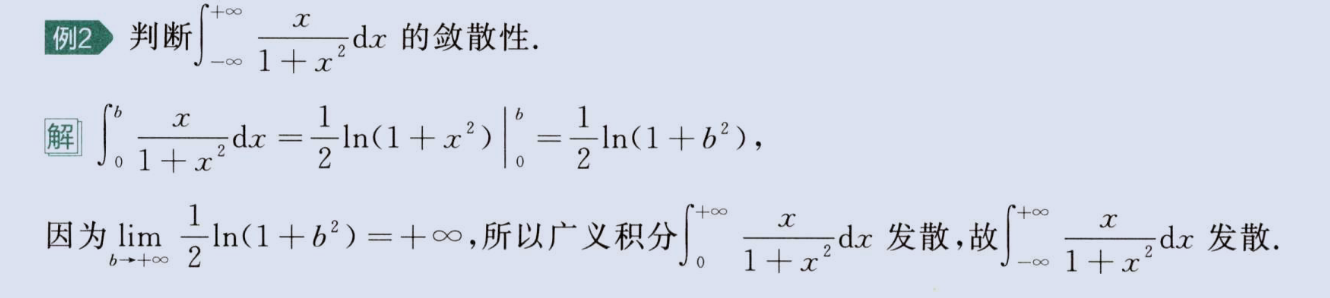image-20230806151613740
广义积分敛散性（积分区间有限）
第二类间断点在端点
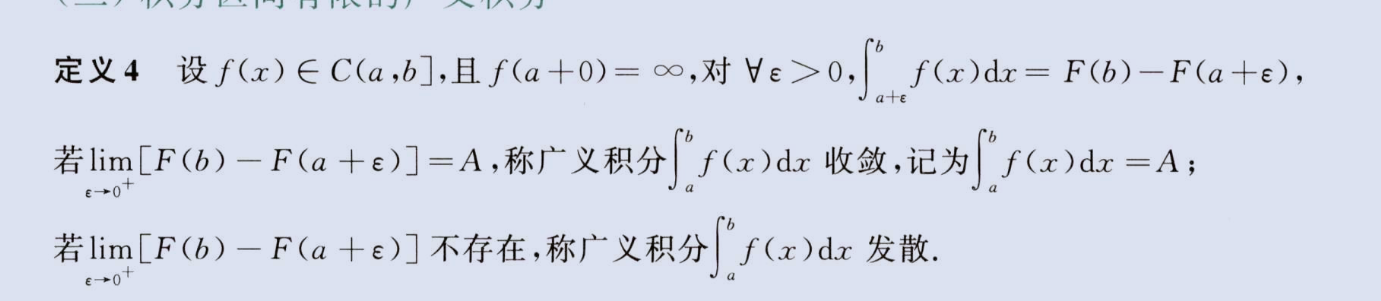image-20230806152242258
第二类间断点在中间
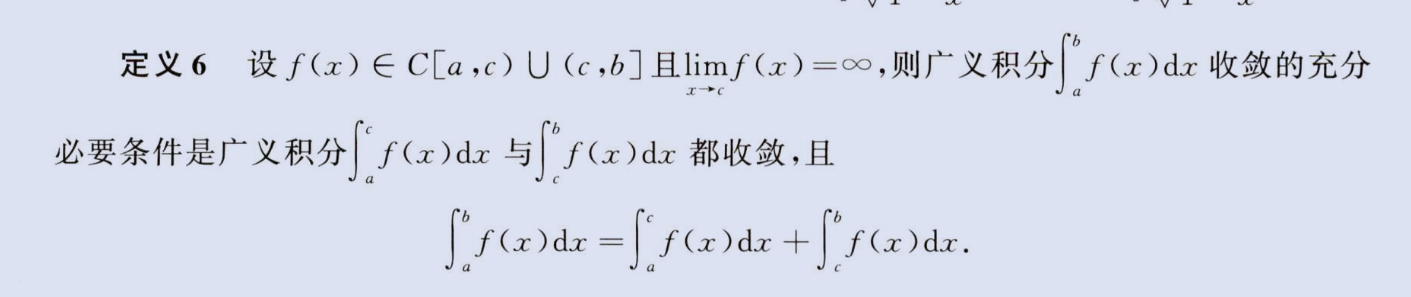image-20230806152421410
广义积分敛散性判别法
1、左无穷、右无穷区间（幂次大于1 收敛）
注意a 和 阿尔法 字母，幂是 阿尔法
image-20230806152858187
2、左无穷、右无穷间断点（幂次小于 1 收敛）
image-20230806153423810
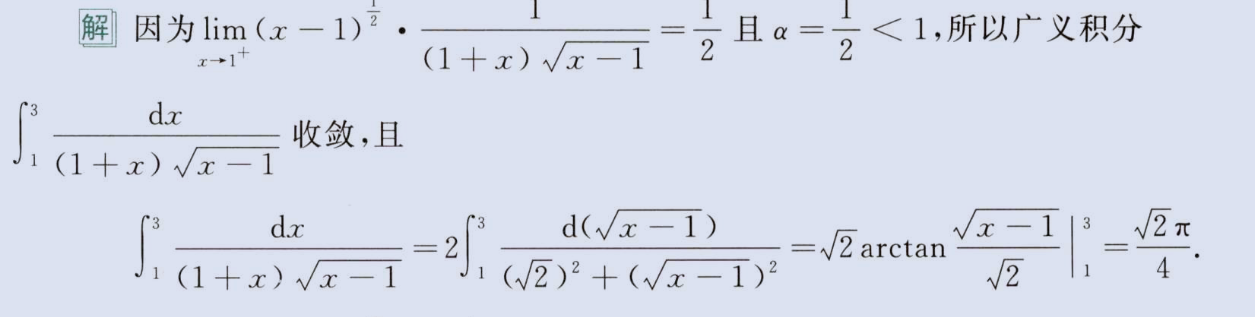image-20230806153742013
3、一边无穷区间，一边无穷间断点
image-20230806153859994
4、放缩证明敛散性
image-20230806154041608
常见的一个反常积分 ┏ 函数
image-20230806154153895
定积分与面积
0、曲线长度（弧微分）
1、直角坐标
2、极坐标
image-20230806154437570
面积微分是三角形底×高
3、旋转曲面与参数方程
image-20230806154646560
面积微分是圆环带，圆环周长×弧微分
定积分与体积
总结：计算截面积，堆砌
image-20230806155416666
题型
定积分加和定义
1、乘积型转化e
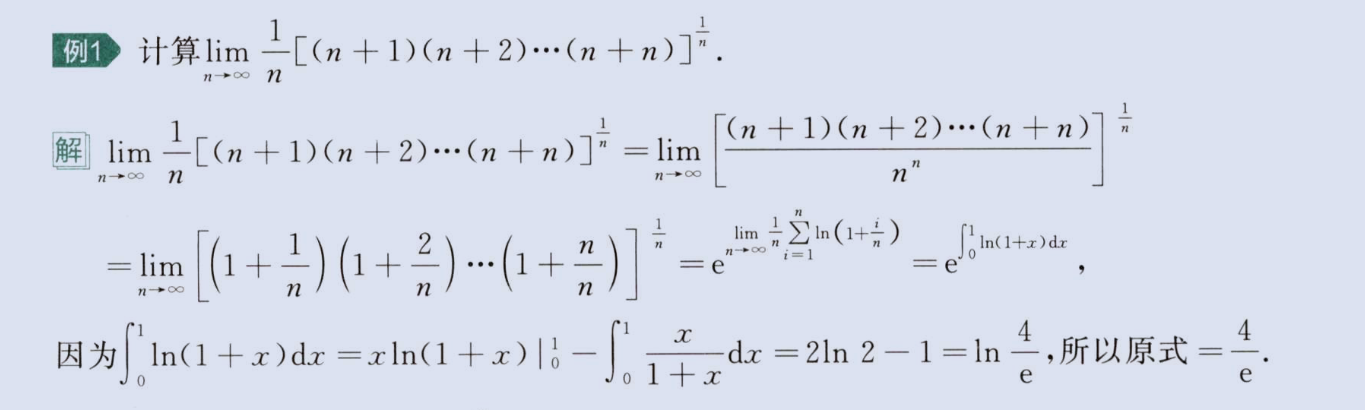image-20230806155607289
2、夹逼定理与积分定义
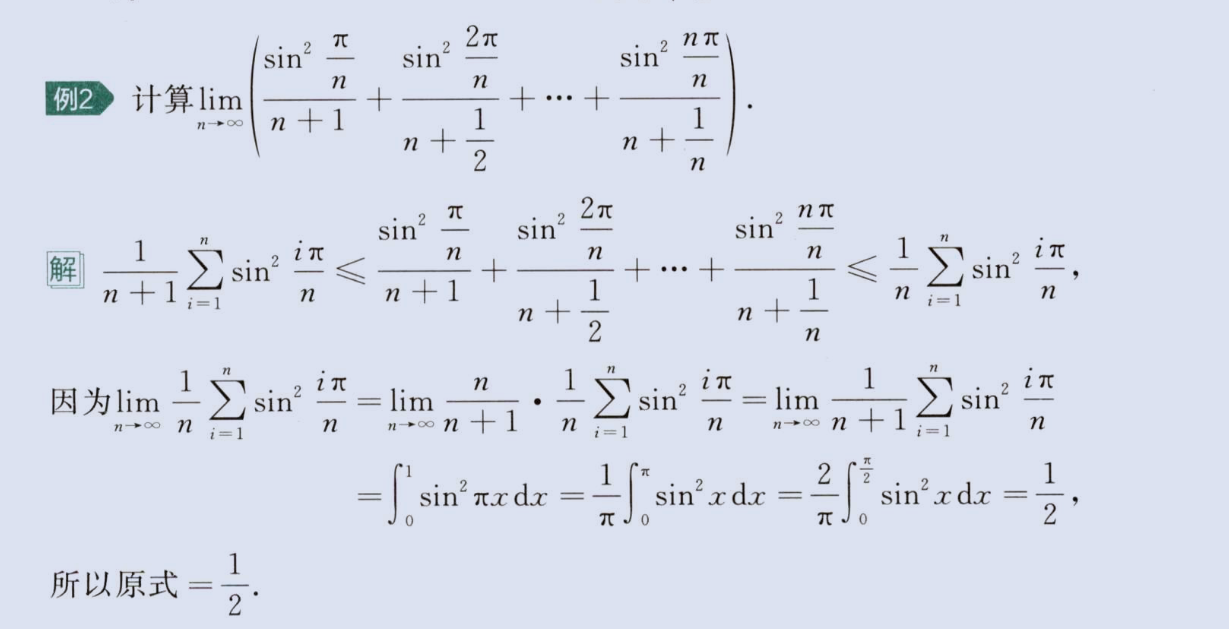image-20230806155737604
不好算的积分与迭代（假设已经计算出来，再凑出一个）
image-20230806160129274
变限
1、换元统一变量
image-20230806160312191
2、与微分方程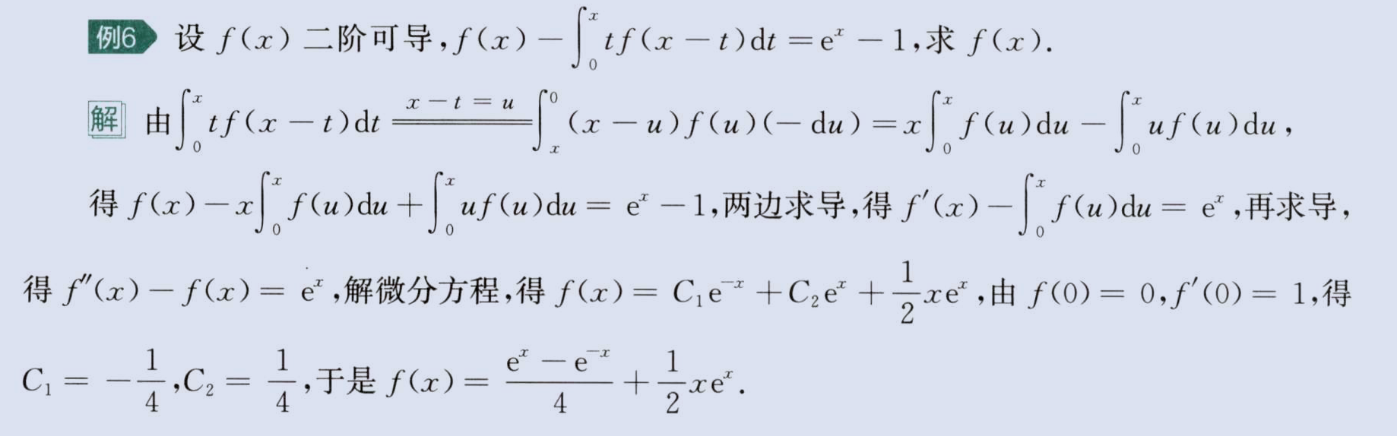 
3、与二重积分
image-20230806160711146
4、凑三角
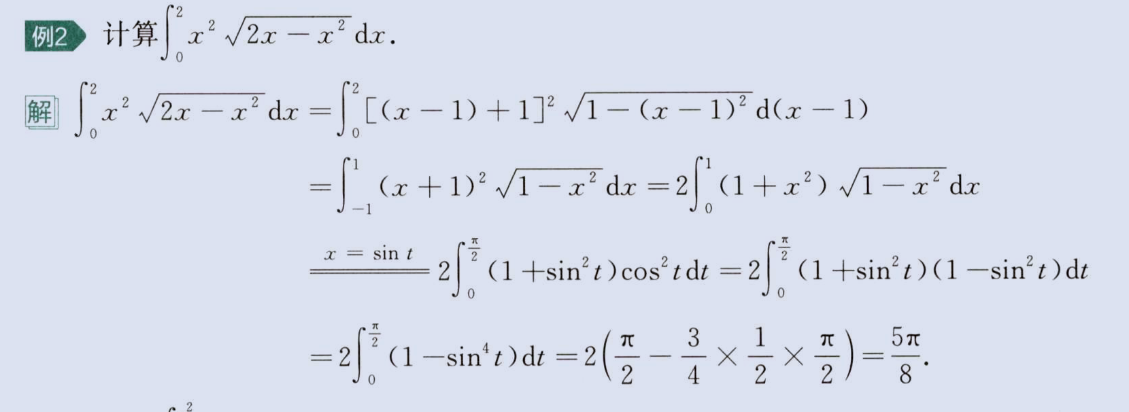image-20230806160829864
三角轮换(sinx与cosx
，tanx与cotx 转换)
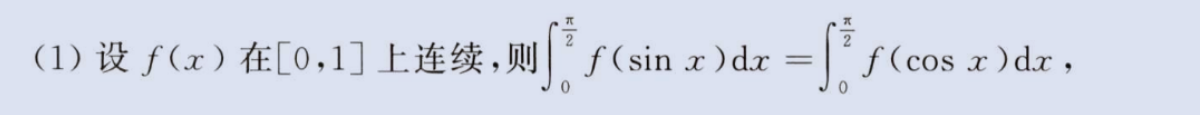image-20230806161218588
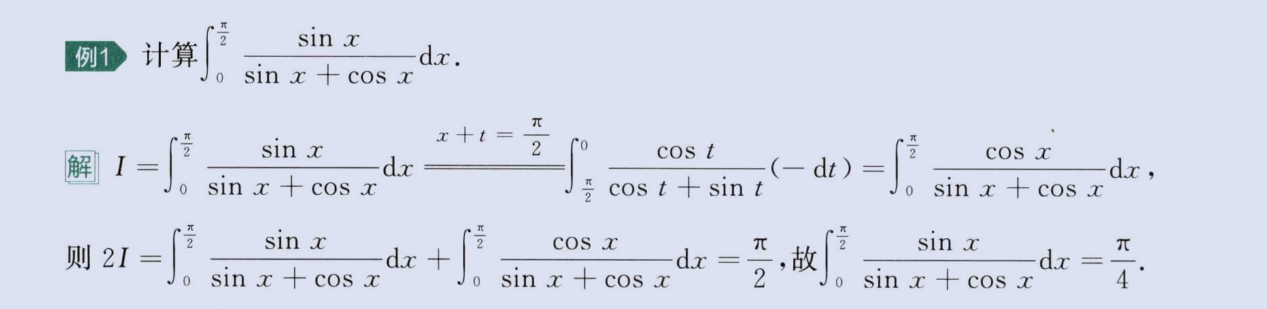image-20230806161138568
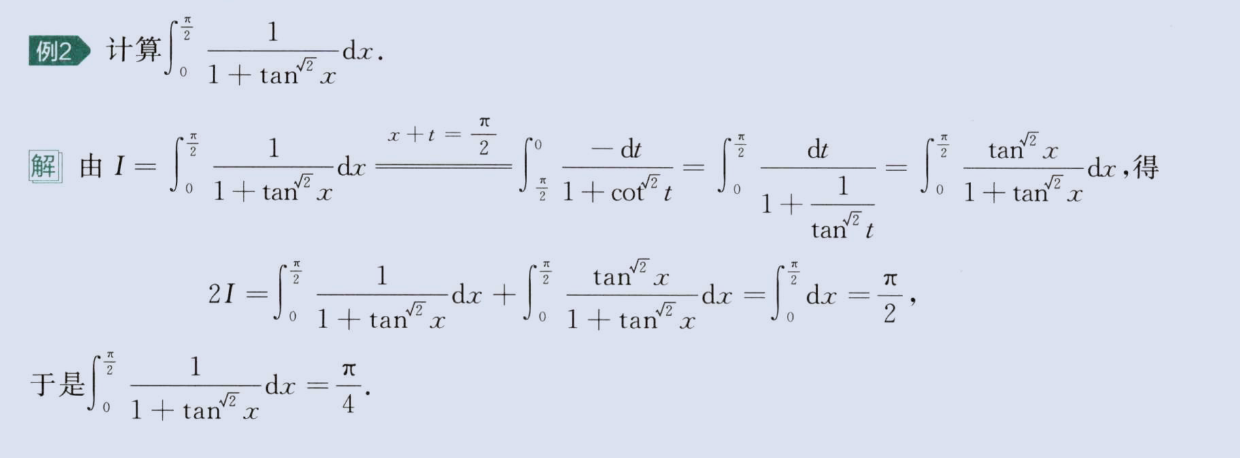image-20230806161529250
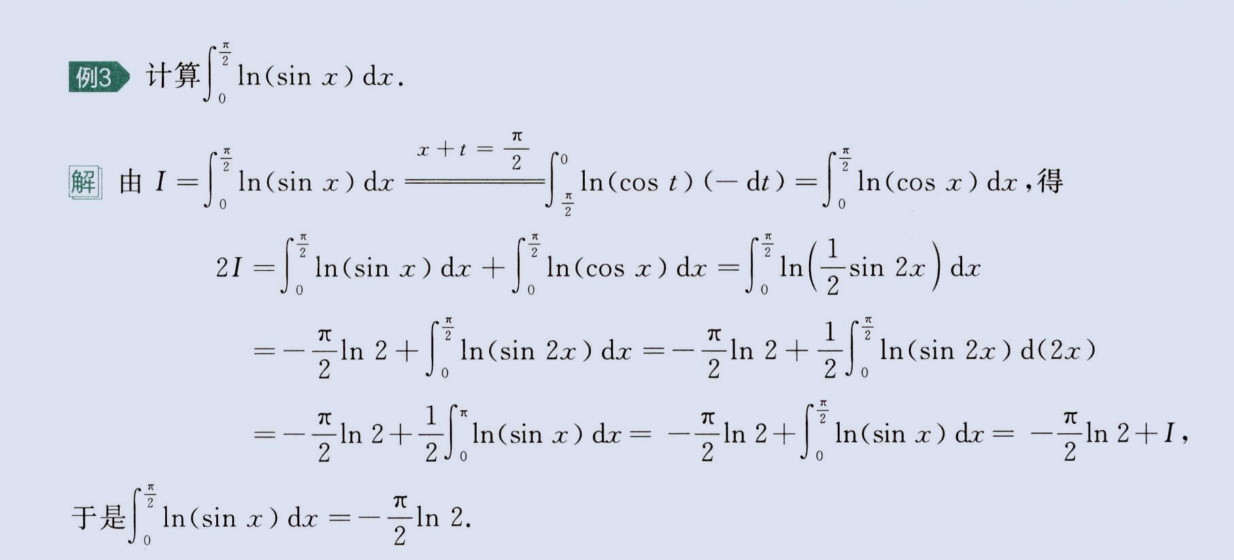image-20230806161659560
分部积分
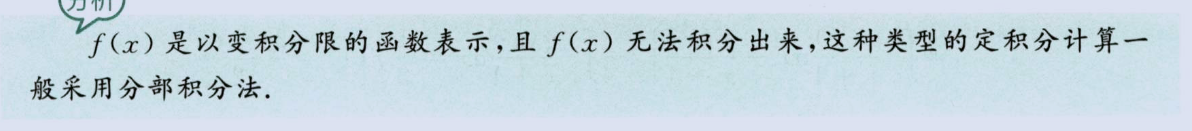image-20230806161801354
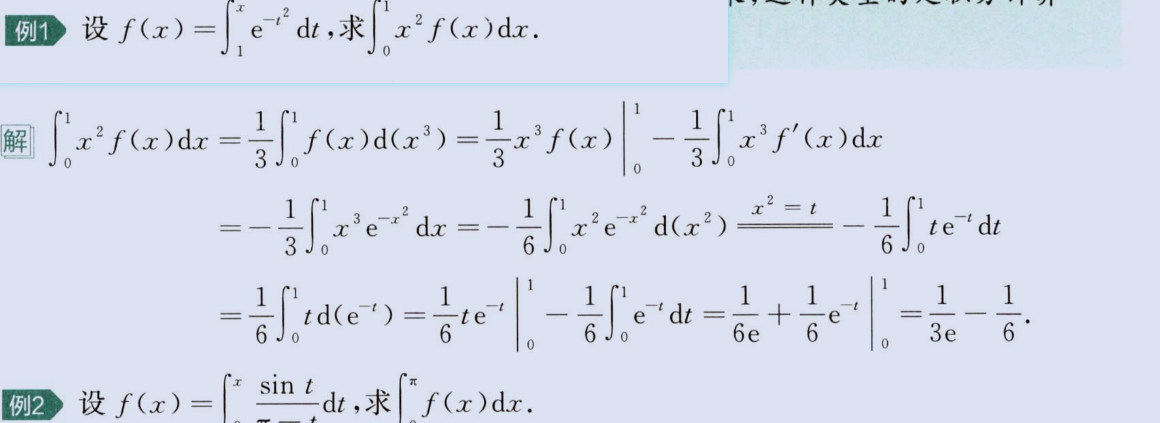image-20230806161859724
证明题
image-20230806162534642
证明题 1-连续函数
a、区间变换
image-20230806162745744
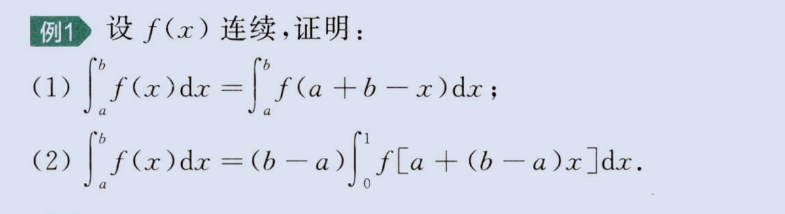
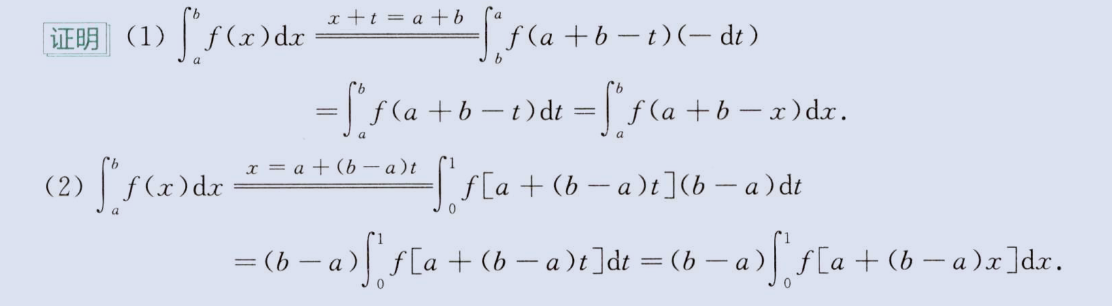image-20230806162800098
b、统一定积分
image-20230806163123766
image-20230806163210136
c、与基本不等式
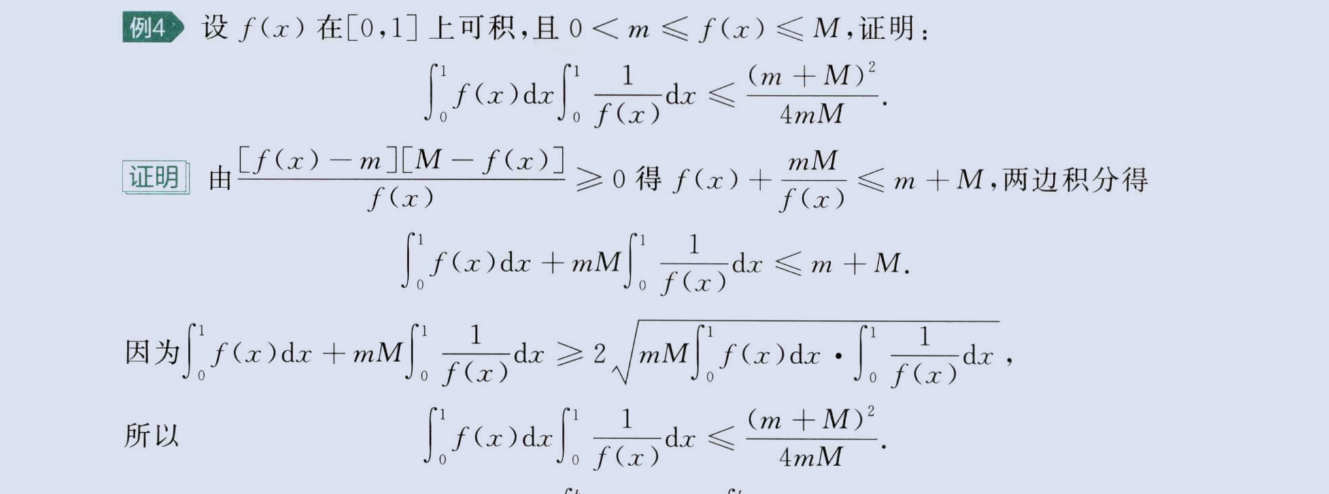image-20230806163846215
d、零点问题与罗尔定理
image-20230806164048287
证明题 2 -连续区间+单调性
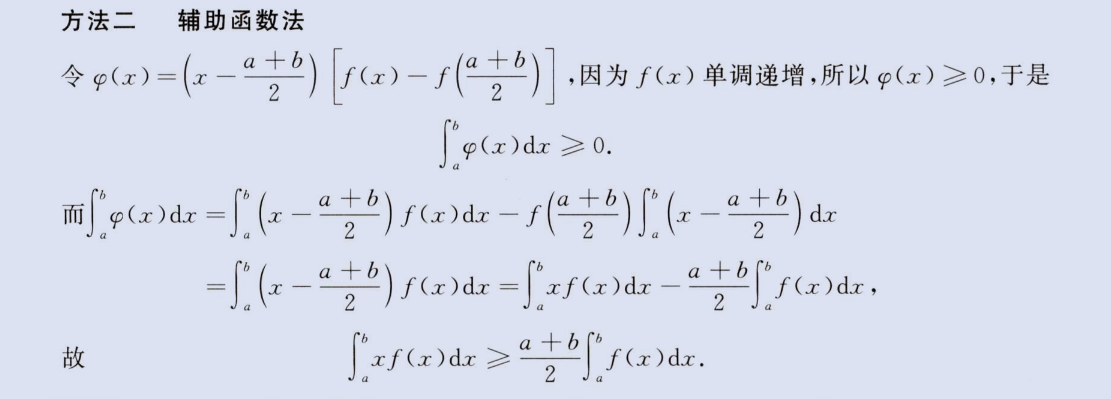image-20230807152427165
上面方法二利用了x-(a+b)/2积分，两个平方差公式，积出来刚好为0
image-20230807152811332
上面方法二利用积分区间分割与积分中值定理配凑出（1-a）的公因式
证明题 3 -周期函数（平移性质）
image-20230807153204985
image-20230807153331661
证明题 4 -连续可导
image-20230807153539623
a、拉格朗日
image-20230807153551952
image-20230807153726774
b、牛顿-莱布尼兹公式（反向应用）
image-20230807153850685
c、积分中值定理+牛顿-莱布尼兹（同一个中值x0的应用）
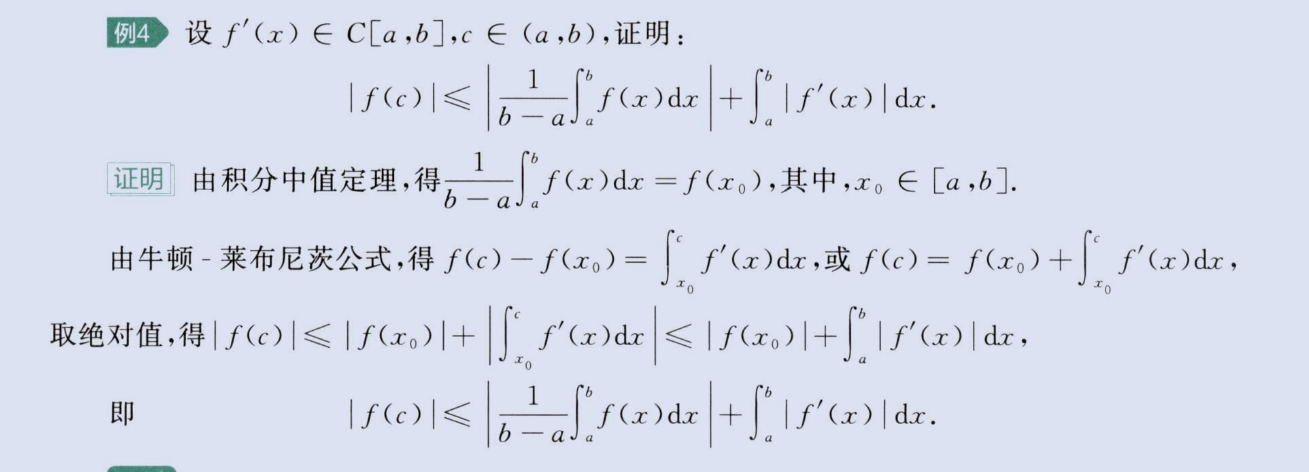image-20230807154118439
d、积分中值定理+罗尔定理
image-20230807154642751
e、积分中值定理+拉格朗日
image-20230807154912995
证明题 5 -高阶导数
image-20230807155059408
a、F(x)泰勒展开+牛莱公式
image-20230807155124368
b、f(x)泰勒展开
image-20230807155527887
c、f(x)泰勒展开+单调性（最后一项的正负问题、从而进行放缩）
image-20230807155616450
广义积分
分段积分，从间断点断开
image-20230807160103988
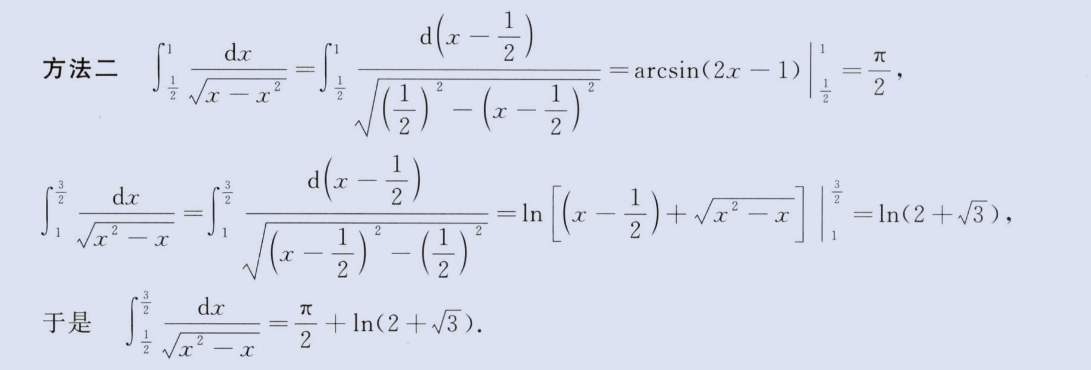image-20230807160124556
定积分应用
image-20230807160407318
