第三章 向量组

线性代数 第三章 向量组 (flowus.cn)

知识点

线性相关和线性无关

image-20230816094502545

判别线性相关性的定理

image-20230816094850471

极大线性无关组

image-20230816094929711

等价向量组

image-20230816095009336

向量组的秩

image-20230816095029326

image-20230816101714013

题型

线性相关性

1、一组线性无关的向量添入一个向量，向量组线性相关，则新添入的向量可以用原来的向量组线性表出

image-20230816103055294

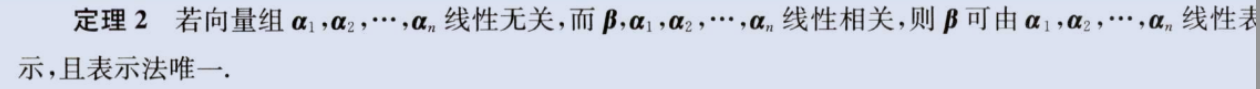
（1）方法一直接定理2，方法二用定义把定理2证明一遍

2、行列式不为 0 线性无关

image-20230816103706305

​ 3、向量组个数超过向量维数，向量组线性相关

image-20230816104013290

4、最原始的定义，存在不全为0的系数让向量组加权相加为0，线性相关

image-20230816104057627

5、反证法+凑条件形式

image-20230816104221320

极大线性无关组

1、向量组矩阵化阶梯矩阵求极大线性无关组

找出能构成唯一零解行列式的向量组，即为极大线性无关组

image-20230816105143776

image-20230816105002806

行变换之后，变换后向量的线性关系不变（系数不变）

image-20230816105646058

秩的证明题

1、一组向量组能被另一组向量组线性表出，前者的秩一定不大于后者

image-20230816105811559

image-20230816110522768

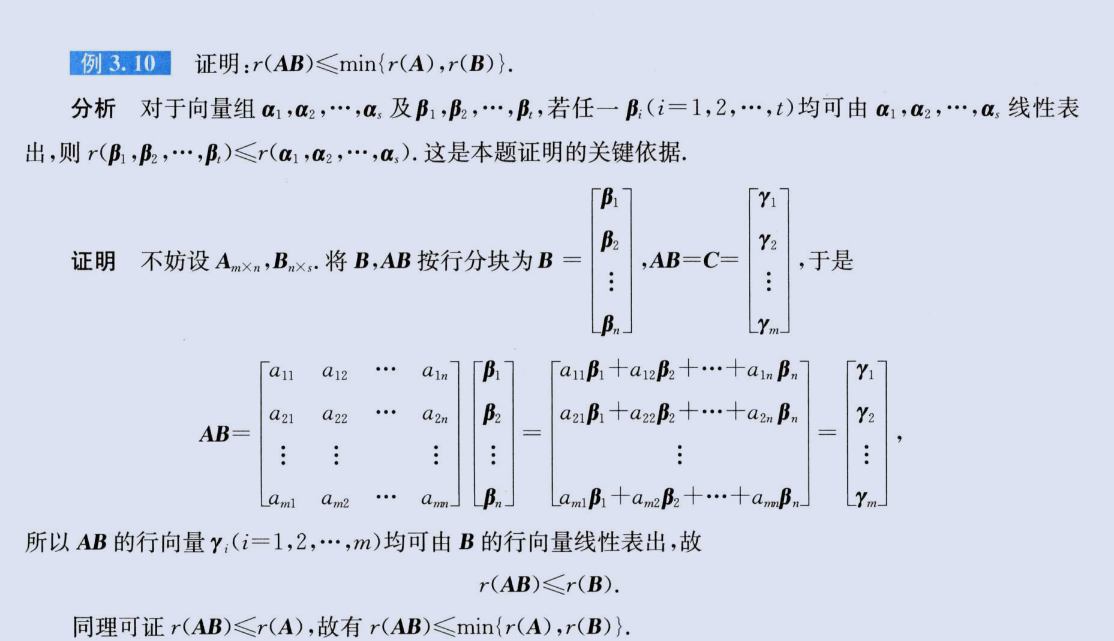
2、伴随矩阵的秩

秩大于等于1实际上等价于行列式中至少一个非0元素

image-20230816112515164

AA*=O 用方程的思想，A伴随看成A x =0 的解向量集合，而由 r(A)=n-1 知道 Ax=0 基础解系由一个向量，A的伴随中最多只有一个线性无关的向量

或者说A 的秩为 r, Ax = 0 的解向量构成的矩阵秩不超过 n-r ，r(A)+r(A*) <= n ，这不是恒成立的，而是 把 A的伴随成齐次线性方程组解的子集

等价矩阵与等价向量组区别与联系

image-20230816115250697

1、矩阵等价要求 同型+ 秩相等 ，向量组等价要求相互线性表出

image-20230816115400048

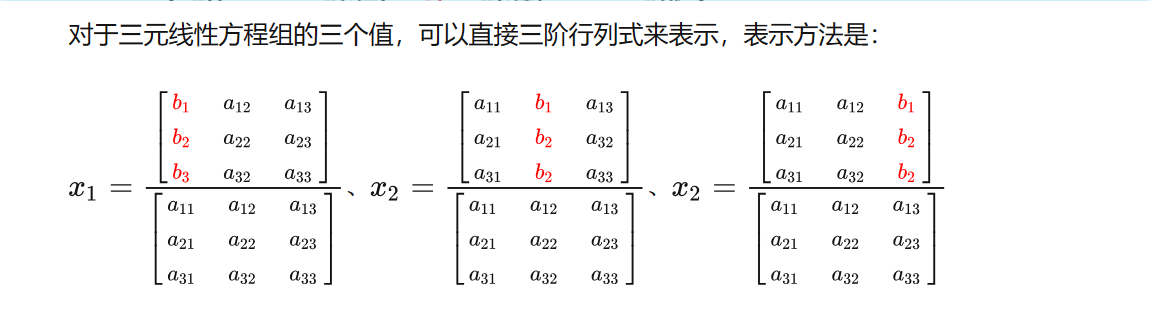
2、克拉默法则解方程组

image-20230816115801894

image-20230816115820084

image-20230816120529689