第四章
线性方程组 (flowus.cn)
知识点
齐次线性方程组
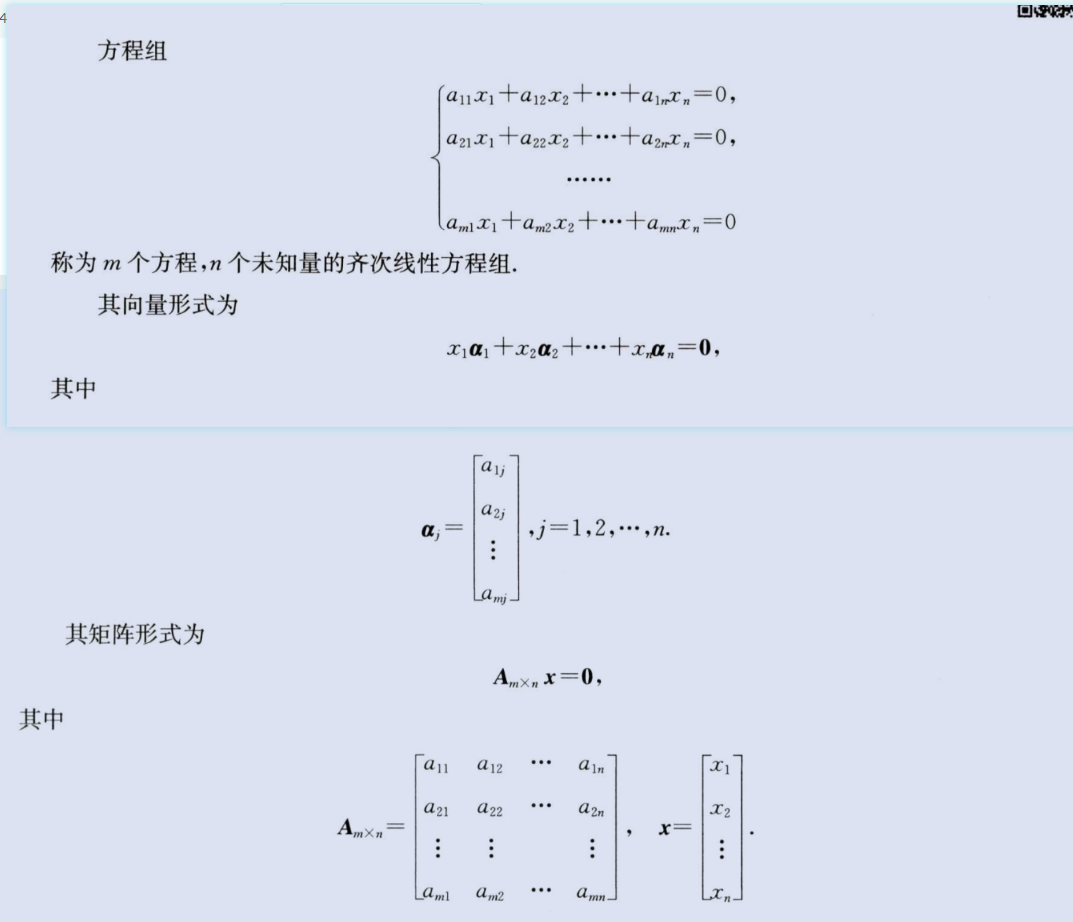image-20230818165117997
齐次线性方程组的解
image-20230818165304097
image-20230818165328600
非齐次方程组
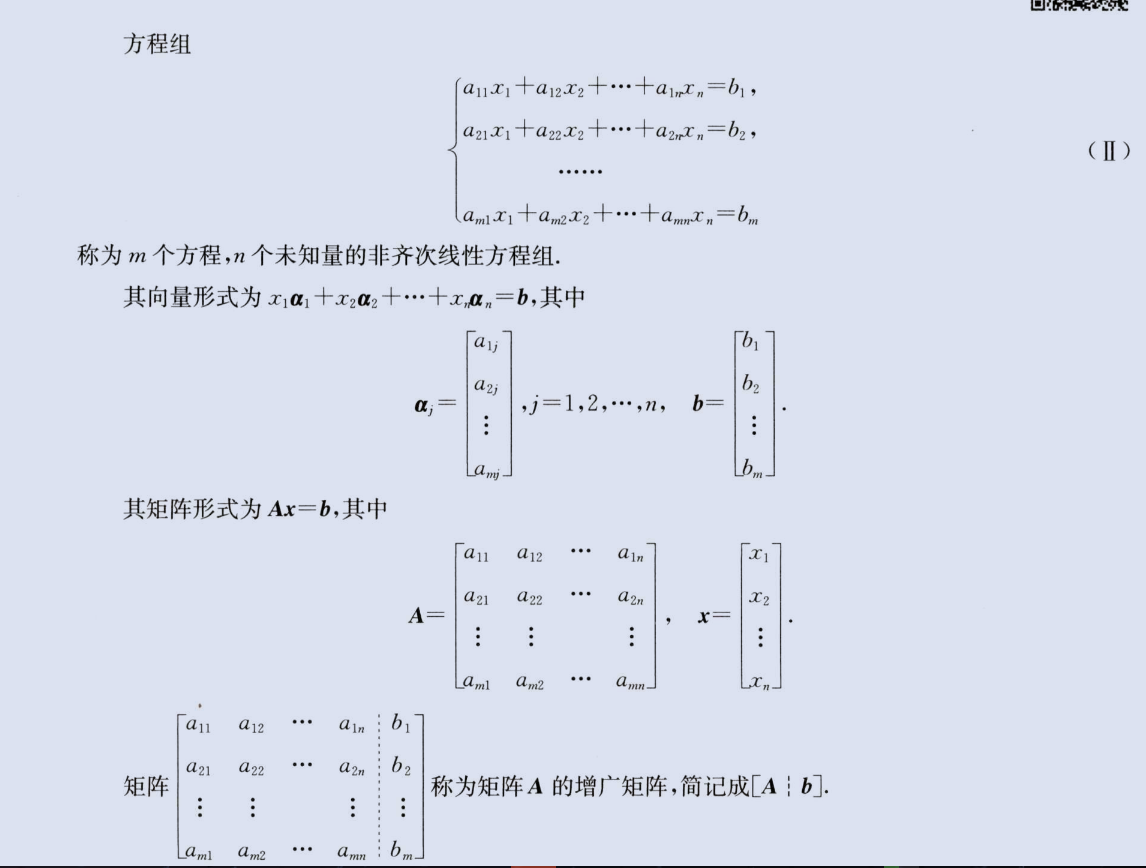image-20230818165639651
image-20230818165703838
题型
解齐次线性方程组
image-20230818172309339
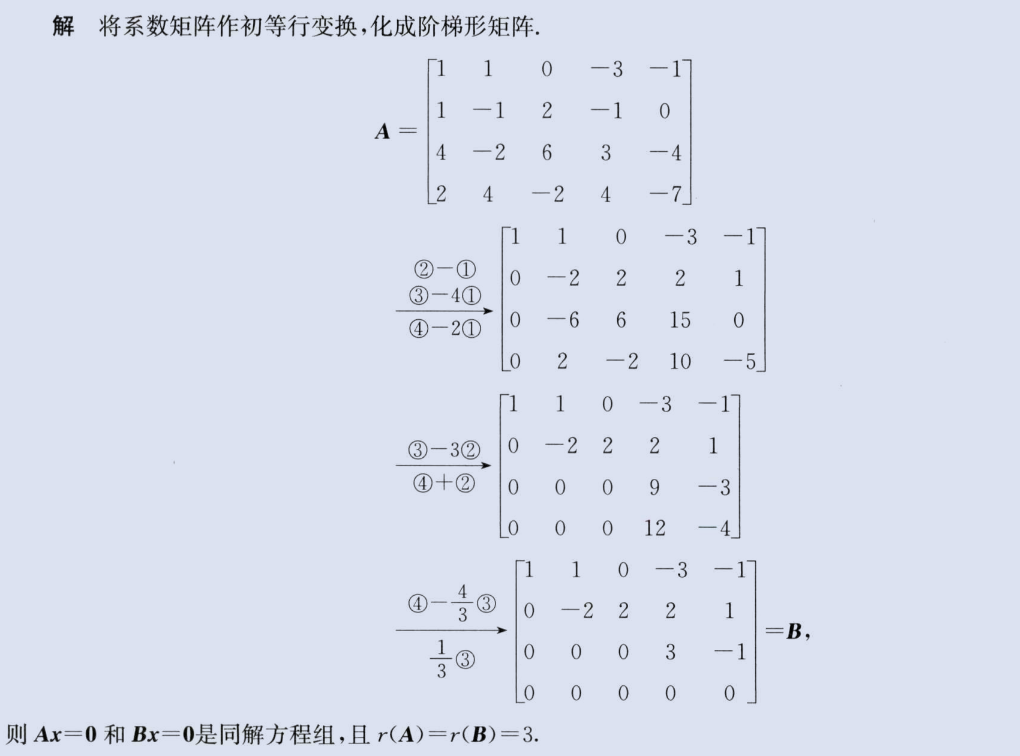image-20230818172428574
image-20230818172610097
image-20230818172643712
关于 n-r 的由来的思考，如果方程组系数矩阵秩为
r=n,那么化为阶梯矩阵之后可以快速推得每个未知数都应该取 0 ，方程只有 0
解，如果方程组系数矩阵 A 的秩 r <
n，那么方程组的未知数取值显然可以是多样的，不一定全是 0
，为了求解这样的方程，我们假定了 n-r 个
自由未知变量，实际上是把这些未知变量变为常数 ，变成了
r阶非齐次线性方程组（且系数矩阵秩为 r），在 n-r
个自由变量当作常数的情况下，我们得到了唯一解，这时把自由变量当作未知数，那么会得到
n-r 个基础解系向量。
非齐次线性方程组
1、解非齐次线性方程组 - 增广矩阵
image-20230818173630872
image-20230818173717784
2、非齐次线性方程组是否有解 增广矩阵的秩是否等于系数矩阵的秩
image-20230818173933108
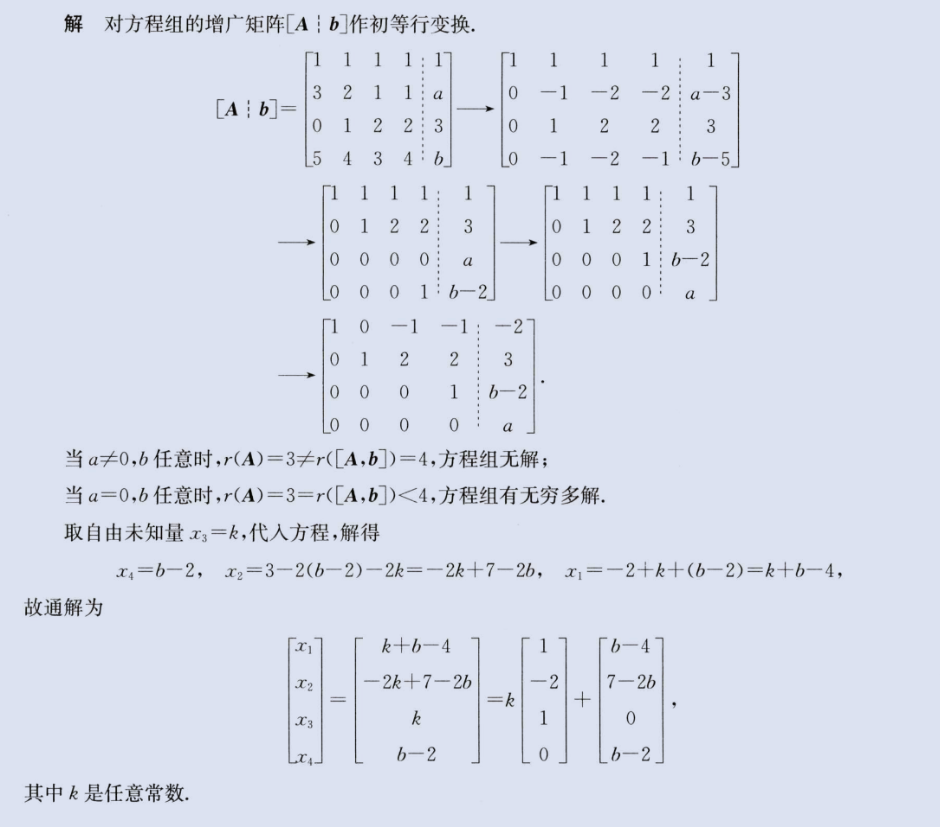image-20230818174014115
方程组是否有解
image-20230818174342050
image-20230818174405403
解的结构
image-20230818174512280
image-20230818174628062
image-20230818174641818
齐次方程组基础解系
image-20230818175021923
1、与伴随矩阵关系
image-20230818175203241
2、基础解系向量右乘系数矩阵，若秩不变，得到新的基础解系
image-20230818175428828
方程组系数矩阵列向量和解的关系
image-20230818175747661
image-20230818180226466
image-20230818180341239
两个方程组公共解
image-20230818180441458
image-20230818180531444
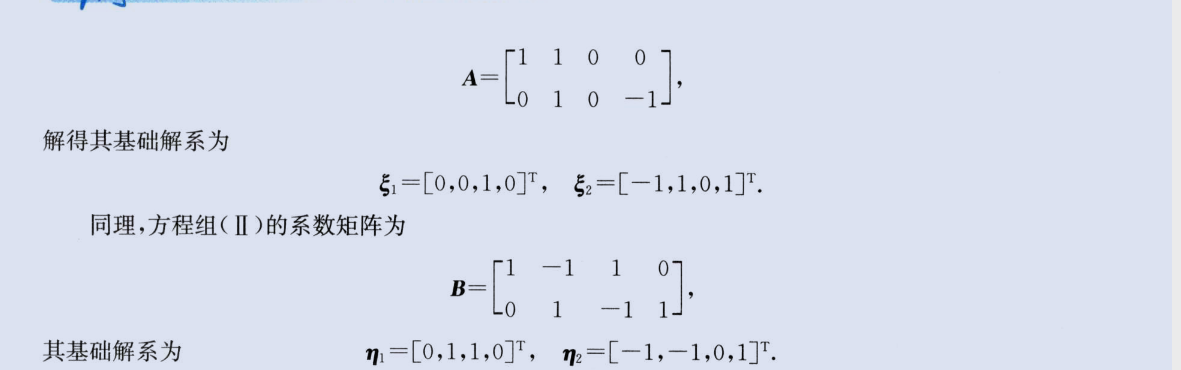image-20230818180544767
image-20230818180640695
image-20230818180722087
同解方程组
image-20230818181019958
image-20230818181106728
image-20230818181127973
image-20230818181204421
