一、绘制单一频率余弦时域图像及其频谱

采样率fs=10kHz（采样间隔Ts=1/10000），采样点N=1000

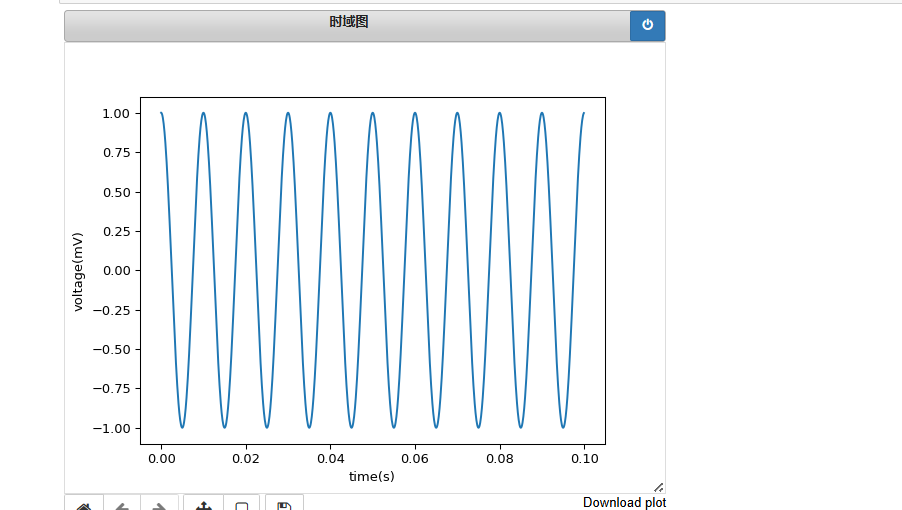
时域

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
%matplotlib notebook

# 采样点
N=1000
# 采样间隔
Ts=1.0/10000.0
# 信号频率
f1=100.0
#离散时间
t=np.linspace(0,N*Ts,N,endpoint=False)
U=np.cos(2.0*np.pi * f1 *t)

plt.figure(num="时域图")
plt.xlabel("time(s)")
plt.ylabel("voltage(mV)")
plt.plot(t,U)
plt.show()


image-20240924213539619

1、numpy.linespace(起点，终点，点数)

关键词：均匀分割

通过定义均匀间隔创建数值序列。其实，需要指定间隔起始点、终止端，以及指定分隔值总数（包括起始点和终止点）；最终函数返回间隔类均匀分布的数值序列。

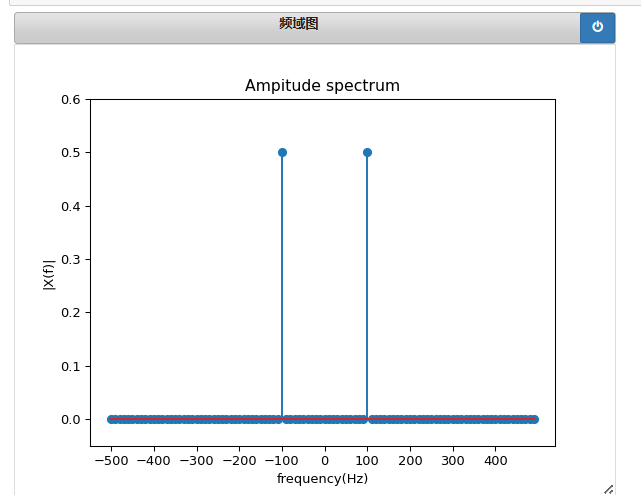
频域

接上部分代码

1
2
3
4
5
6
7
8
9
10
11
12
13
from scipy.fft import fft,fftfreq,fftshift
yf = fft(U,N)/N
yf = np.abs(yf)
yf = fftshift(yf)
xf = fftshift(fftfreq(N,Ts))
plt.figure(num="频域图")
plt.stem(xf,yf)
plt.xlim(-500,500)
plt.xticks(np.arange(-500,500,100))
plt.xlabel("frequency(Hz)")
plt.ylabel("|X(f)|")
plt.title("Ampitude spectrum")
plt.show()
image-20240924215656063

参考

numpy中的fft和scipy中的fft，fftshift以及fftfreq_np.fft.fftshift 和 np.fft.fft 的区别-CSDN博客

1、scipy.fftshift(fft后需要重新排布的序列)

numpy和scipy中都有fftshift，用于将FFT变换之后的频谱显示范围从[0, N]变为：

[-N/2,N/2]或者[-(N-1)/2,(N-1)/2] (N为奇数)

2、scipy.fftfreq(n=采样点，d=采样周期)

在画频谱图的时候，要给出横坐标的数字频率，这里可以用fftfreq给出，对于fftfreq的说明如下：

scipy.fftpack.fftfreq(n, d=1.0)

第一个参数n是FFT的点数，一般取FFT之后的数据的长度（size）

第二个参数d是采样周期，其倒数就是采样频率Fs，即d=1/Fs

需要说明的是，DFT变换中，频率的分辨率为Fs/n=1/d*n

fftfreq得到的结果为各个数字频率 kFs/n = k/dn

3、matplotlib.pyplot.stem(x向量，y向量)

绘制棉棒图

stem 从基线到 Y 坐标绘制垂直线，并在尖端放置一个标记

4、matplotlib.pyplot.xlim(x轴绘制下限，x轴绘制上限)

matplotlib.pyplot.ylim(y轴绘制下限，y轴绘制上限)

5、matplotlib.pyplot.xticks(x轴刻度向量)

matplotlib.pyplot.yticks(y轴刻度向量)

6、numpy.arange(起点，终点，步长)

NumPy的arange函数用于创建指定范围和步长的等差数组。它可以接受1到3个参数，分别表示起点、终点和步长。

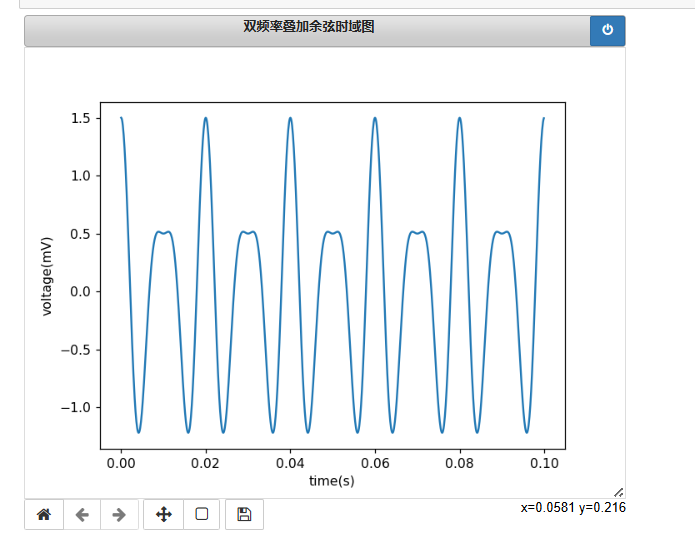
二、绘制双频率余弦函数时域图像及频谱

时域

接上代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 采样点
N=1000
# 采样间隔
Ts=1.0/10000.0
# 信号频率
f1=100.0
f2=150.0
#离散时间
t=np.linspace(0,N*Ts,N,endpoint=False)
U1=np.cos(2.0*np.pi * f1 *t)
U2=np.cos(2.0*np.pi * f2 *t)
U=U1+0.5*U2
plt.figure(num="双频率叠加余弦时域图")
plt.xlabel("time(s)")
plt.ylabel("voltage(mV)")
plt.plot(t,U)
plt.show()

image-20240924231733623

频域

接上代码 

1
2
3
4
5
6
7
8
9
10
11
12
13
from scipy.fft import fft,fftfreq,fftshift
yf = fft(U,N)/N
yf = np.abs(yf)
yf = fftshift(yf)
xf = fftshift(fftfreq(N,Ts))
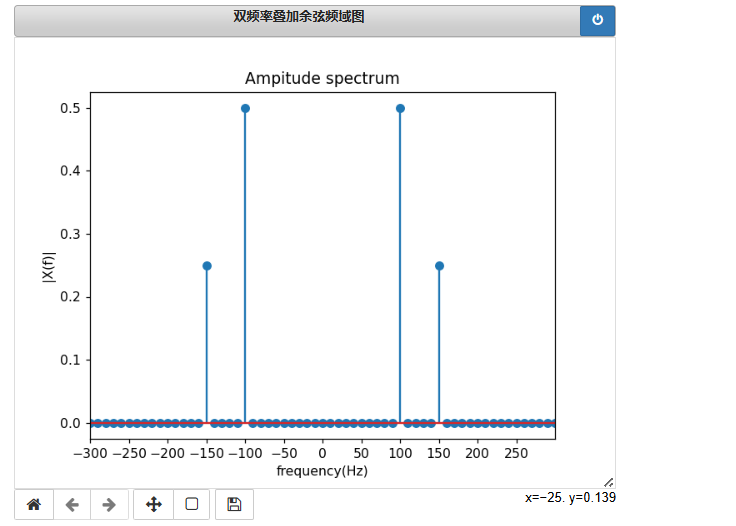
plt.figure(num="双频率叠加余弦频域图")
plt.stem(xf,yf)
plt.xlim(-300,300)
plt.xticks(np.arange(-300,300,50))
plt.xlabel("frequency(Hz)")
plt.ylabel("|X(f)|")
plt.title("Ampitude spectrum")
plt.show()

image-20240924231755592

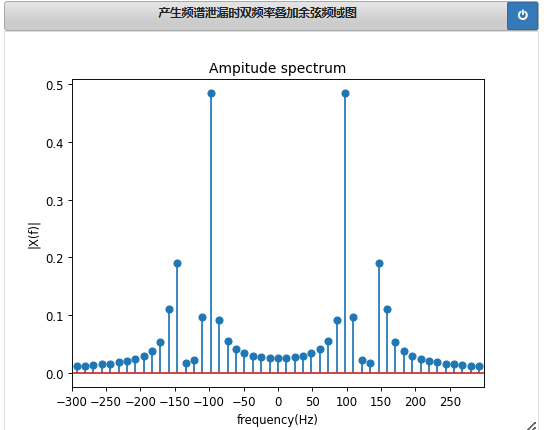
三、频谱泄漏

产生频谱泄漏原因：截取到的信号不是完整周期，产生高频信号

频域

1
2
3
4
5
6
7
8
9
10
11
12
13
N1=820
yf = fft(U,N1)/N1
yf = np.abs(yf)
yf = fftshift(yf)
xf = fftshift(fftfreq(N1,Ts))
plt.figure(num="产生频谱泄漏时双频率叠加余弦频域图")
plt.stem(xf,yf)
plt.xlim(-300,300)
plt.xticks(np.arange(-300,300,50))
plt.xlabel("frequency(Hz)")
plt.ylabel("|X(f)|")
plt.title("Ampitude spectrum")
plt.show()
image-20240925232442496

改为连续点作图如下：

plt.stem(xf,yf)改为plt.plot(xf,yf)

image-20240925232627547

四、频率分辨力

fs/N = 1/L，即频率分辨率只和采样时间有关

(NTs=L,L为采样时间)

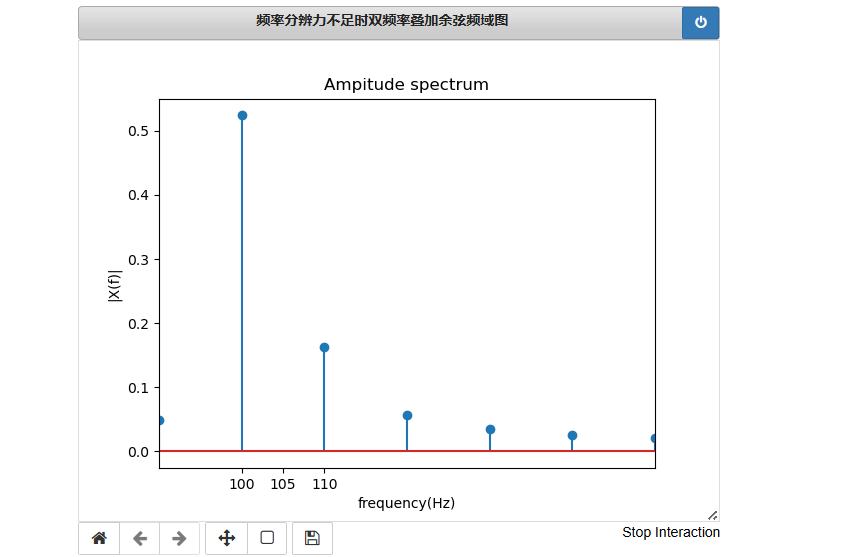
一种频率分辨力不足的情形

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 采样点
N=1000
# 采样间隔
Ts=1.0/10000.0
# 信号频率
# 频率分辨力为fs/N=1/(NTs)=10 Hz,相差为2的频率分量无法分辨
f1=100.0python
f2=105.0
t=np.linspace(0,N*Ts,N,endpoint=False)
U1=np.cos(2.0*np.pi * f1 *t)
U2=np.cos(2.0*np.pi * f2 *t)
U=U1+0.5*U2
plt.figure(num="100Hz和105Hz频率叠加余弦时域图")
plt.xlabel("time(s)")
plt.ylabel("voltage(mV)")
plt.plot(t,U)
plt.show()

下图中为100Hz和105Hz信号的叠加时域图

image-20240926001030367

频率分辨力为10Hz，无法分辨两个频率分量 

1
2
3
4
5
6
7
8
9
10
11
12
13

yf = fft(U,N)/N
yf = np.abs(yf)
yf = fftshift(yf)
xf = fftshift(fftfreq(N,Ts))
plt.figure(num="频率分辨力不足时双频率叠加余弦频域图")
plt.stem(xf,yf)
plt.xlim(90,150)
plt.xticks(np.arange(100,115,5))
plt.xlabel("frequency(Hz)")
plt.ylabel("|X(f)|")
plt.title("Ampitude spectrum")
plt.show()

image-20240926002147794